Wheel Graphs with Integer Edges
Wheel Graphs with Integer Edges
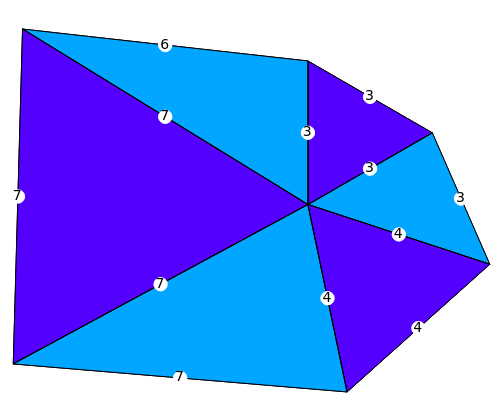
Harborth's conjecture states that the edges of any planar graph can all have integer length. Planar graphs with non-triangular faces can have edges added to get a maximal planar (or triangulated) graph, where all faces are triangles. A solution for a given maximal planar graph would contain many integer wheel graphs. This Demonstration shows many integer wheel graphs found with searches. Triangles are colored by their area radicals.
(Update for 2023). The number under the radical in a triangle area is known as the triangle's characteristic. This Demonstration seems to show that the maximum number of different triangle characteristics in an integer wheel graph is two. In 2021, Gábor Damásdi proved that an integer wheel graph can have at most two characteristics[5]. In addition, it's impossible for all the edge lengths to be odd.
Details
Details
Examining the =282429536481 hexagon possibilities took weeks, despite excluding many types of symmetries. A fast method to collect allowable heptagons, octagons, and general -gons with a given maximal edge length is currently unknown to the author.
12
9
n
References
References
[2] Wikipedia. "Planar Graph." (Mar 1, 2015) en.wikipedia.org/wiki/Planar_graph# Maximal_planar _graphs.
[5] Gábor Damásdi, "Odd Wheels Are Not Odd-Distance Graphs." Disc. & Comp. Geom. vol 69, pp327–337, 2023. https://link.springer.com/article/10.1007/s00454-021-00325-0.
External Links
External Links
Permanent Citation
Permanent Citation
Ed Pegg Jr
"Wheel Graphs with Integer Edges"
http://demonstrations.wolfram.com/WheelGraphsWithIntegerEdges/
Wolfram Demonstrations Project
Published: March 4, 2015