Energies for a Heaviside-Lambda Potential Well
Energies for a Heaviside-Lambda Potential Well
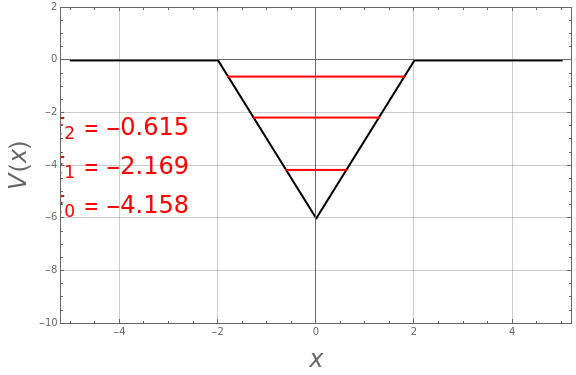
This Demonstration calculates the bound energy levels of a particle in an inverted Heaviside-lambda (vee-shaped) potential well of depth and width , using the semiclassical Wentzel–Kramers–Brillouin (WKB) method. The numerical results are within 1% of the values that would be obtained from the exact solutions of the corresponding Schrödinger equation. The energies are determined by the Sommerfeld–Wilson quantization conditions . With , the integral reduces to , noting that are the classical turning points. This can be solved for the energy levels: =-+, . The highest bound state is given by =-+, where is the floor, which for positive numbers is simply the integer part.
V
0
2a
∮h
2m[E-V(x)]
dq=n+1
2
ℏ=m=1
4
a(1+E/)
V
0
∫
0
E+-x
dxV
0
V
0
a
x=±a1+
E
V
0
E
n
V
0
1/3
2
4
2/3
3π
V
0
a
2/3
n+
1
2
n=0,1,2,…,
n
max
n
max
1
2
4a
2
V
0
3π
⌊⌋
Details
Details
External Links
External Links
Permanent Citation
Permanent Citation
S. M. Blinder
"Energies for a Heaviside-Lambda Potential Well"
http://demonstrations.wolfram.com/EnergiesForAHeavisideLambdaPotentialWell/
Wolfram Demonstrations Project
Published: January 6, 2011