Sampling Theorem

$Aborted

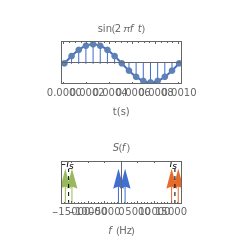
The top figure shows a sine wave of frequency

f

and its samples. The bottom figure shows the Fourier spectrum

S(f)

of the sampled signal. It consists of two spectral lines at

±f

, repeated periodically at integer multiples of the sampling rate

f

s

.

According to the sampling theorem, for

f≤

f

s

/2

, the samples uniquely represent the sine wave of frequency

f

. For

f>

f

s

/2

, aliasing occurs, because the replicated spectra begin to overlap. In the range

0≤f≤

f

s

/2

, a spectral line appears at the frequency

|f-

f

s

|

. In the upper figure the sine wave with the corresponding frequency and color appears.

Note that for

f

s

=8kHz

and

f>6kHz

, additional lines at

-f+2

f

s

and

f-2

f

s

appear in the spectrum.