Enthalpy and Entropy Departure Functions for Gases
Enthalpy and Entropy Departure Functions for Gases
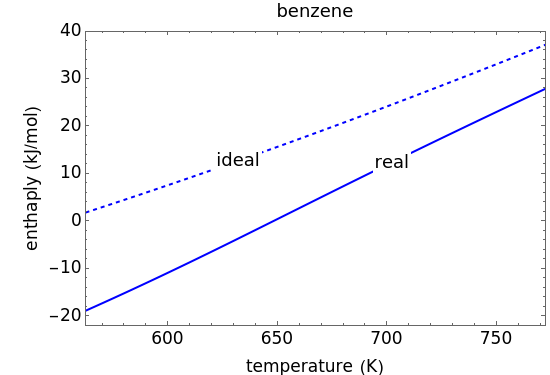
This Demonstration plots the enthalpies and entropies for a real gas and an ideal gas as a function of temperature, relative to a reference state at a selected pressure and temperature, using the Peng–Robinson equation of state and ideal-gas heat capacities. Select argon, benzene, or carbon dioxide with buttons. For each gas, the temperature scale is adjusted so the plots are only shown above the critical temperature. Select enthalpy or entropy departure function, which is the difference between the thermodynamic property (enthalpy, entropy) for a real gas and an ideal gas at the same temperature and pressure. You can vary the pressure with the slider. Select "compare departure functions" to view departure functions for all three gases as a function of temperature at 10 MPa. Click "show labels" to label each departure function curve with the corresponding gas.
Details
Details
Enthalpy and entropy are calculated using the Peng–Robinson equation of state (EOS) for a real gas and the ideal gas law for an ideal gas:
H
S
H=(H-)+-+
ig
H
ig
H
ig
H
R
ig
H
R
S=(S-)+-+
ig
S
ig
S
ig
S
R
ig
S
R
where is in kJ/mol and is in kJ/[mol K]; the superscript represents an ideal gas, the subscript refers to the reference state, and and are the enthalpy and entropy departure functions for a real gas calculated from the Peng–Robinson EOS, while and are the ideal gas enthalpy and entropy at the reference state.
H
S
ig
R
(H-)
ig
H
(S-)
ig
S
ig
H
R
ig
S
R
-=(T-)+-+-+-
ig
H
ig
H
R
Cp
A
T
R
1
2
Cp
B
2
T
2
T
R
1
3
Cp
C
3
T
3
T
R
1
4
Cp
D
4
T
4
T
R
-=ln(T/)+(T-)+-+--Rln(P/)
ig
S
ig
S
R
Cp
A
T
R
Cp
B
T
R
1
2
Cp
C
2
T
2
T
R
1
3
Cp
D
3
T
3
T
R
P
R
where , , , and are heat capacity constants (), is temperature (K), and is pressure (MPa).
Cp
A
Cp
B
Cp
C
Cp
D
Cp=+T++
Cp
A
Cp
B
Cp
C
2
T
Cp
D
3
T
T
P
(H-)=RTZ-1-(1+κ
ig
H
A
2
2
BTr/α
)lnZ+(
2
+1)BZ-(
2
-1)B(S-)=Rln(Z-B)-κ
ig
S
AR
2
2
BTr/α
lnZ+(
2
+1)BZ-(
2
-1)BTr=T/Tc
κ=0.375+1.542ω-0.270
2
ω
α=
2
(1+κ(1-
Tr
))where is the compressibility factor, is the reduced temperature (dimensionless, not to be confused with ), is the critical temperature (K), is the acentric factor, and and are constants.
Z
Tr
T
R
Tc
ω
κ
α
A=0.457α
Pr
2
Tr
B=0.0778
Pr
Tr
Pr=P/Pc
where and are constants, is the reduced pressure (dimensionless, not to be confused with ), and is the critical pressure (MPa).
A
B
Pr
P
R
Pc
These equations are used to calculate the compressibility factor :
Z
Z=+
1/3
-q2+
r
1/3
-q2-
r
r=4+/27
2
q
2
m
q=2-+2727
3
a
2
a
2
a
1
a
0
m=3-3
a
1
2
a
2
where , , , , , and are constants used for simplification.
q
r
m
a
2
a
1
a
0
a
2
a
1
2
B
a
0
2
B
3
B
The screencast video at[1] explains how to use this Demonstration.
References
References
[1] Enthalpy and Entropy Departure Functions for Gases. www.colorado.edu/learncheme/thermodynamics/EntropyEnthalpyDepartureFunctions.html.
Permanent Citation
Permanent Citation
Rachael L. Baumann, Neil Hendren, John L. Falconer, Derek M. Machalek, Nathan S. Nelson, Garrison J. Vigil
"Enthalpy and Entropy Departure Functions for Gases"
http://demonstrations.wolfram.com/EnthalpyAndEntropyDepartureFunctionsForGases/
Wolfram Demonstrations Project
Published: May 13, 2015