A Multiway Model of Chemical Reactions
A Multiway Model of Chemical Reactions
Ariana-Dalia Vlad
Harvard University
This project aims to create a multiway model of chemical reactions through molecular rewriting, with tokens representing compounds and events representing reactions. Applying a self-perpetuating pattern reaction to different inputs can result in either known compounds or molecules not available in common databases (such as PubChem). Similar path numbers distributions are obtained for the graphs regardless of their starting compound, suggesting that this is a characteristic of the multicomputation rule and not the input. There was no significant difference between the number of paths available to reach molecules depending on their availability in PubChem. Creating a more realistic model and analyzing a larger dataset of graphs in the future will allow us to study polymerization, drug design, and biochemical pathways more in depth.
Section 1: Self-Perpetuating Reactions
Section 1: Self-Perpetuating Reactions
In this project, we consider a reaction self-perpetuating if it can be applied again to the product. We choose such reactions in our work because they guarantee an infinite graph. The key to specifying self-perpetuating reactions in the Wolfram language is the PatternReaction function.
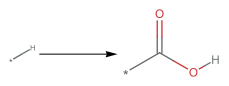
PatternReaction["[*:3][C:1](=[O:2])[O][H]>>[*:3][C:1](=[O:2])[N]([H])([H])"]
Out[]=
The above reaction represents the formation of an amide group from a carboxyl group. However, the way it is specified, the reaction is applied to the pattern on the left, rather than a specific reactant. Then, replacing the star (*) with any radical, we obtain the wanted transformation. We can start with Arginine as the reactant.
MoleculePlot@Molecule["Arginine"]MoleculePlot@First@ApplyReaction[PatternReaction["[*:3][C:1](=[O:2])[O][H]>>[*:3][C:1](=[O:2])[N]([H])([H])"],{Molecule["Arginine"]}]
Out[]=
Out[]=
We see that the reaction has been applied correctly, but it is not self-perpetuating. We obtain this characteristic by pairing it with the Carboxylation of a radical.
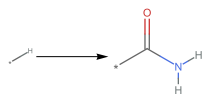
Carboxylation = PatternReaction["[*:3][H]>>[*:3][C](=[O])[O][H]"]
Out[]=
The product of the second reaction is the same as the reactant of the first, hence if put together they form a two-step pattern reaction. The amide group contains two Hydrogens that can be further Carboxylated, making the total reaction self-perpetuation too. This is the rule we will further use in the multiway system.
In[]:=
totalrxn=PatternReaction["[*:1][H]>>[*:1][C](=[O])[N]([H])([H])"]
Out[]=
Section 2: Multiway Systems
Section 2: Multiway Systems
The multiway system is based on the predilection of the reactant pattern in chemical compounds and the fact that the product contains at least two such patterns. Then, the obtained graph is growing with every step and more and more molecules are obtained. Let’s start with a simple example.
In[]:=
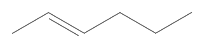
MoleculePlot@Molecule["CC=CCCC"]MoleculeSubstructureCountMolecule["CC=CCCC"],First@["Reactants"]
Out[]=
Out[]=
12
The substructure count looks for the defined pattern in the initial molecule, and gives us the number of sites where the rule can be applied. Because the pattern appears 12 times in the input molecule, we expect to obtain 12 compounds after applying the totalrxn rule once. However, because the molecule is symmetric, not all outputs will be distinct. It is clear then that to create a correct model of chemical rewriting, we need to filter the results. We will eliminate the molecules that don’t respect valence rules and delete the duplicate compounds.
deleteDuplicateProducts[products:{___Molecule}]:=DeleteDuplicates[products,MoleculeMatchQ];deleteDuplicateProducts[productSets:{{___Molecule}...}]:=DeleteDuplicates[productSets,And@@MapThread[MoleculeMatchQ,{##}]&];filterBadValence=ReplaceAll[{m_Molecule/;Length[m["ValenceErrors"]>0]}:>Sequence[]];
We create the graphs using the Resource Functions available.
Out[]=
In[]:=
graph1={mol_}:>Flatten@@ApplyReaction,{mol},All//,,3,"EventVertices" -> False, "TokenDeduplication"->True,"TokenEquivalenceFunction"MoleculeMatchQ,"TokenLabeling"True,"TokenEquivalenceFunction"->MoleculeMatchQ,"TokenRenderingFunction"(MoleculePlot[#,ImageSize->30]&),EdgeStyle -> Directive[{Arrowheads[0.01], Opacity[0.35]}], GraphLayout"RadialEmbedding",ImageSize->12 72,AspectRatio0.75
Out[]=
Section 3: Graph Analysis
Section 3: Graph Analysis
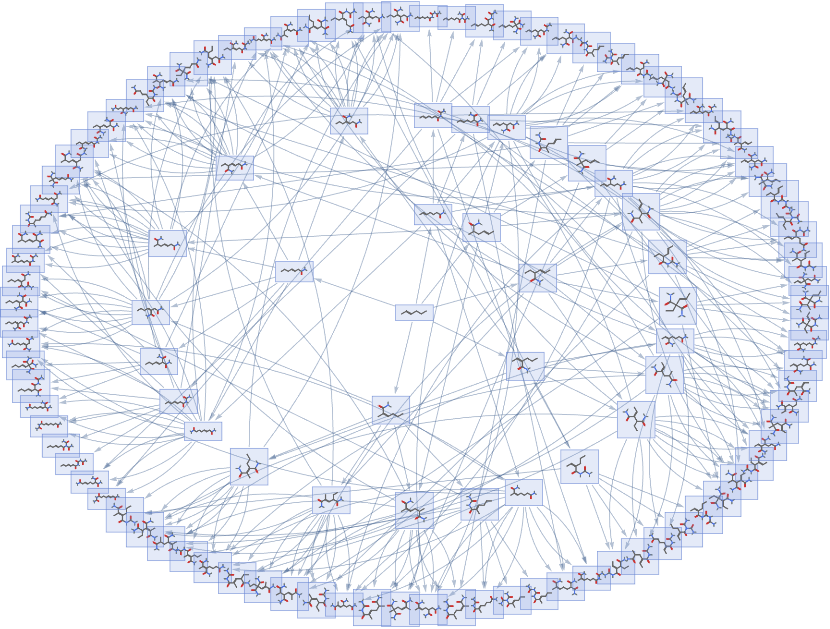
To properly understand the relation between the obtained compounds and the multiway graphs’ structure, we will compare four such systems which use the same rule but a different starting molecule.
In[]:=
MoleculePlot@Molecule["C/C[C@@H]1[C@H](C)C=CC1=O"]MoleculeSubstructureCountMolecule["C/C[C@@H]1[C@H](C)C=CC1=O"],First@["Reactants"]
Out[]=
Out[]=
12
In[]:=
graph2={mol_}:>Flatten@@ApplyReaction,{mol},All//,,3,"EventVertices" -> False,"TokenDeduplication"->True,"TokenEquivalenceFunction"MoleculeMatchQ,"TokenLabeling"True,"TokenEquivalenceFunction"->MoleculeMatchQ,"TokenRenderingFunction"(MoleculePlot[#,ImageSize->30]&),EdgeStyle -> Directive[{Arrowheads[0.01], Opacity[0.35]}], GraphLayout"RadialEmbedding",ImageSize->12 72,AspectRatio0.75
First, we will check which of the obtained molecules are contained in the PubChem database.
Since we can find known PubChem molecules up to the second iteration, the rule must be a reaction that occurs in Chemistry. This is proven again by starting with Methane, which results in known compounds up to the fourth step. However, if we start from the second molecule, none of the outputs are in PubChem. More analysis is needed to say whether this unknown molecules are impossible to create or are just missing from the database. We can also look into the number of paths that reach one molecule(considering only the first three graphs, as they have the same number of patterns in the initial molecule).
Although we start with three different molecules, we obtain very similar distributions for the number of paths possible for each outer molecules. This suggests that this is a property of the self-perpetuating reaction and depends on the pattern exclusively. Looking only at the first and fourth graphs, we see that the number of paths to a molecule does not seem to depend on its presence in the PubChem database. However, this dataset is not large enough for a general conclusion to be drawn.
Concluding Remarks
Concluding Remarks
While the work on molecular rewriting and chemical multicomputation is only at the beginning, we can already predict their usefulness in high-throughput analysis of chemical reactions. This project presents the fundamentals of creating a multiway system with a self-perpetuating pattern reaction as the rule, and broadly discusses the resulting graphs. In the future, more work is needed to refine the system to more realistically model chemical reactions. Then, the results of the multicomputation could teach us about polymerization, drug discovery, biochemical pathways, and more.
Acknowledgment
Acknowledgment
I would like to thank Stephen Wolfram for directing me towards this project, and my mentor James Boyd and my TA Yorick Zeschke for their support, guidance, and the hours they set aside to work with me. Their help was invaluable for someone who started the Winter School with limited knowledge about the Wolfram Language. I would also like to thank Eric James Parfitt, Nik Murzin, and Sotiris Michos for helpful discussion and feedback, and Jason Biggs and Bob Nachbar for providing me with useful code on pattern matching and multicomputation.