In[]:=
SetOptions[$FrontEnd,"DynamicUpdating"->True]Charting`$InteractiveHighlighting=False;
In[]:=
CloudGet["https://www.wolframcloud.com/obj/1eb0b2e2-e756-41a3-b448-da34b26fa278"];(*NPartiteSolverPackageV2*)CloudGet["https://www.wolframcloud.com/obj/308ad6c1-f9d0-4a49-8db8-fa8c2d1dad07"];(*BipartiteEntanglement*)CloudGet["https://www.wolframcloud.com/obj/d558fe48-b922-480d-9866-8e813e6678fd"];(*StabilityMethodsV2*)CloudGet["https://www.wolframcloud.com/obj/fffa5aed-3b59-4bcb-8023-1ab7c3adf193"];(*Helpers*)CloudConnect[];
In[]:=
coresToLaunch=14;CloseKernels[];LaunchKernels[coresToLaunch];
In[]:=
$Assumptions=Element[g0,Reals]&&Element[κ,Reals]&&Element[γouF,Reals]&&Element[ΓouF,Reals]&&Element[δ,Reals]&&Element[Δ,Reals]&&Element[ϵl,Reals]&&Element[η,Reals]&&Element[ν,Reals]&&Element[ΩouF,Reals]&&Element[
κ
,Reals]&&Element[t,Reals];varsTransfer={"A","B"};lindblad=Sqrt[κ]*A1;hamiltonianEquationTransfer=ν*BD1B1+δ*AD1A1+g0*SymbolicMultiplication[η*(B1+BD1),Sm*AD1+Sp*A1,varsTransfer]//Expand;hamiltonianEquationTransferOut[]=
AD1A1δ+AD1B1g0Smη+AD1BD1g0Smη+A1B1g0Spη+A1BD1g0Spη+BD1B1ν
In[]:=
{secondOrderEqns,noTimeNeededSubs,noTimeConjugateSubs}=OZeroEquationsOfMotionNDSolve[2,hamiltonianEquationTransfer,{lindblad},{{A1,AD1,B1,BD1}},{"F"},t,varsTransfer]/.{Sm->-ϵl*Exp[-I*ϕ]/Δ,Sp->-ϵl*Exp[I*ϕ]/Δ}//Refine//Expand;{secondOrderEqnsM,noTimeNeededSubsM,noTimeConjugateSubsM}=OZeroEquationsOfMotionNDSolve[2,hamiltonianEquationTransfer,{lindblad},{{}},{"F"},t,varsTransfer]/.{Sm->-ϵl*Exp[-I*ϕ]/Δ,Sp->-ϵl*Exp[I*ϕ]/Δ}//Refine//Expand;
In[]:=
replacements=Join[noTimeNeededSubs,noTimeConjugateSubs];rotatedSecondOrder=ApplySingleModeRotation[{δ,ν},varsTransfer,2,t,varsTransfer];rotatedSecondOrderDerivatives=(D[#[[1]],t]->D[#[[2]],t])&/@rotatedSecondOrder;fullRotationReplacers=Join[rotatedSecondOrder,rotatedSecondOrderDerivatives];secondOrderDiffSet=Assuming[$Assumptions,Refine[secondOrderEqns[[1]]/.fullRotationReplacers]]//Expand;secondOrderDiffSetM=Assuming[$Assumptions,Refine[secondOrderEqnsM[[1]]/.fullRotationReplacers]]//Expand;
In[]:=
reOrder=ReorderOperators[Reverse[varsTransfer],varsTransfer,2];allPairs=Table[{elt,ToExpression["mean"<>elt],ToExpression["cov"<>elt]},{elt,varsTransfer}];allMeanCovReplacers=Flatten[Table[{elt[[2]]GenerateMeans[{elt[[1]]}]/.replacements,elt[[3]]GenerateCovarianceMatrix[{elt[[1]]}]/.replacements},{elt,allPairs}],1];meanAXP=GenerateMeansXP[varsTransfer[[1]]]/.replacements;meanBXP=(GenerateMeansXP[varsTransfer[[2]]])/.replacements;covAXP=GenerateCovarianceMatrixXP[varsTransfer[[1]]]/.replacements;covBXP=(GenerateCovarianceMatrixXP[varsTransfer[[2]]])/.replacements;meanABXP=GenerateMeansXP[varsTransfer]/.replacements;meanBAXP=(GenerateMeansXP[Reverse[varsTransfer]]/.reOrder)/.replacements;covABXP=GenerateCovarianceMatrixXP[varsTransfer]/.replacements;covBAXP=(GenerateCovarianceMatrixXP[Reverse[varsTransfer]]/.reOrder)/.replacements;
In[]:=
setLaserStrength[tShift_,delta_,coupling_,eta_,tVar_]:=(If[tShift==0,0,((Pi*delta)/(2*eta*coupling*tShift))*HeavisideTheta[tShift-tVar]]);
(*DifferentPulses([t]);E0<<wherer>>1;{gamma,(E0/(1+Exp[gamma*(t-tc)]))}(LogisticFunction,ν>>gammatobefullyvalid);gamma<<;tc=wherer>>1;tTransfer=b+ln-1+whereb>>1;{E0*HeavisideTheta[tShift-t]}(HeavisideTheta,technicallytorapidofashifttobefullyvalid,butsincetShiftshouldequaltTransfer,noharmnofoul?);tShift==tTransferastheoriginalcriteriabecomemorevalid.*)
ϵ
L
ν*Δ
r**η
g
0
ν
r
ln-1+r
π
2
e
ν
r
ν
π
2
e
r*π
2*ν
(*B->AphiL=Pi/2;A->BphiL=-Pi/2;*)
(*ke=2*ReQuietSolve0-F1γou+I*F1δ-++γouΓou++F1F2++F1F3++F1F4
F3g0ϵlη
ϕ
Δ
F4g0ϵlη
ϕ
Δ
2
F1
κ
+1
2
κ
-I*F1Ωou,0-F2γou-I*F2δ-F3g0ϵlη
-ϕ
Δ
F4g0ϵlη
-ϕ
Δ
κ
-I*F2Ωou,0-F3γou-F1g0ϵlη
-ϕ
Δ
F2g0ϵlη
ϕ
Δ
κ
+I*F3ν-I*F3Ωou,0-F4γou-F1g0ϵlη
-ϕ
Δ
F2g0ϵlη
ϕ
Δ
κ
-I*F4ν-I*F4Ωou/.{t0},{F1,F2,F3,F4}[[1]][[1]][[2]]^2;*)In[]:=
paramsLaserFixed=<|Δ.001,g0.001,η.001,ϕ->Pi/2|>//Values;
In[]:=
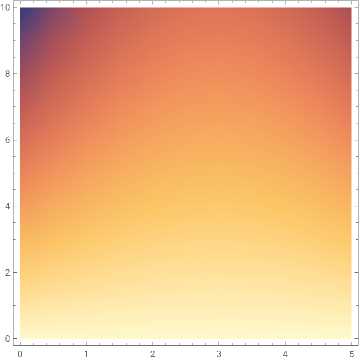
rawData=ParallelTable[tShift=45;inits=GenerateInitialSingleComboConditions[2,{{"B","CS",Sqrt[n]*Exp[I*Pi/2],0}},varsTransfer];paramsLaserCurrent=Join[{setLaserStrength[tShift,paramsLaserFixed[[1]],paramsLaserFixed[[2]],paramsLaserFixed[[3]],t]},paramsLaserFixed];paramsSystem=Join[<|ν->5,κ->k0,γouF->0.5,ΩouF->0,ΓouF->1|>//Values,paramsLaserCurrent];Tmax=tShift+10;Block[{ϵl=paramsSystem[[6]],Δ=paramsSystem[[7]],δ=paramsSystem[[1]],ν=paramsSystem[[1]],g0=paramsSystem[[8]],η=paramsSystem[[9]],κ=paramsSystem[[2]],γouF=paramsSystem[[3]],ΩouF=paramsSystem[[4]],ΓouF=paramsSystem[[5]],ϕ=paramsSystem[[10]]},testNM=NDSolve[Join[secondOrderDiffSet//Expand,inits],secondOrderEqns[[2]],{t,0,Tmax},PrecisionGoal10,AccuracyGoal10,MethodAutomatic][[1]];testM=NDSolve[Join[secondOrderDiffSetM//Expand,inits],secondOrderEqns[[2]],{t,0,Tmax},PrecisionGoal10,AccuracyGoal10,MethodAutomatic][[1]];];{numn,kappak0,fidNMSwapQuiet[CalculateGaussianFidelity[{Re[(meanABXP/.{ttShift})/.(testNM/.{ttShift})]//Chop,Re[(covABXP/.{ttShift})/.(testNM/.{ttShift})]//Chop},{Re[(meanBAXP/.testNM)/.{t0}]//Chop,Re[(covBAXP/.testNM)/.{t0}]//Chop}]],fidMSwapQuiet[CalculateGaussianFidelity[{Re[(meanABXP/.{ttShift})/.(testM/.{ttShift})]//Chop,Re[(covABXP/.{ttShift})/.(testM/.{ttShift})]//Chop},{Re[(meanBAXP/.testM)/.{t0}]//Chop,Re[(covBAXP/.testM)/.{t0}]//Chop}]]},{n,0,1000,1000/10},{k0,0,5*10^(-3),(5*10^(-3))/10},DistributedContexts->All,ProgressReporting->True,Method->"FinestGrained"];
In[]:=
ListDensityPlot[{#[[2]]*10^(3),#[[1]]*10^(-2),#[[3]]}&/@(Flatten[rawData//Values,1]),PlotLegendsAutomatic]
Out[]=