WOLFRAM NOTEBOOK

Hydrogenic Atoms: The Radial Component

Radial Component

The radial component of the wavefunction shows how the wavefunction varies with distance, r, from the nucleus. It depends on the quantum number n and l.
The list below provides a summary of the radial components for orbitals 1s (n=1, l=0) through 3d (n=3, l=2).
1s=
R
1,0
(r)=2
3/2
Z
a
0
−Zr/
a
0
e
​​2s=
R
2,0
(r)=
1
8
3/2
Z
a
0
2−
Zr
a
0
−Zr/2
a
0
e
​​2p=
R
2,1
(r)=
1
24
3/2
Z
a
0
Zr
a
0
−Zr/2
a
0
e
​​3s=
R
3,0
(r)=
2
81
3
3/2
Z
a
0
27−18
Zr
a
0
+2
2
Zr
a
0
−Zr/3
a
0
e
​​3p=
R
3,1
(r)=
2
81
6
3/2
Z
a
0
6
Zr
a
0
+
2
Zr
a
0
−r/3
a
0
e
​​3d=
R
3,2
(r)=
2
81
30
3/2
Z
a
0
2
Zr
a
0
−Zr/3
a
0
e

Wolfram Wavefunctions

In[]:=
RComp={{"Orbital","Radial"},{"1s",2(Z/52.9)^(3/2)*E^(-Z*r/52.9)},{"2s",(1/8)^(1/2)*(Z/52.9)^(3/2)*(2-Z*r/52.9)*E^(-Z*r/(52.9))},{"2p",(1/24)^0.5*(Z/52.9)^(3/2)*(Z*r/52.9)*E^(-Z*r/(2*52.9))},{"3s",(2/(81*Sqrt[3]))*(Z/52.9)^(3/2)*(27-18*Z*r/52.9+2*(Z*r/52.9)^2)*E^(-Z*r/(3*52.9))},{"3p",(2/(81*Sqrt[6]))*(Z/52.9)^(3/2)*(6*Z*r/52.9-(Z*r/52.9)^2)*E^(-Z*r/(3*52.9))},{"3d",(2/(81*Sqrt[30]))*(Z/52.9)^(3/2)*((Z*r/52.9)^2)*E^(-Z*r/(3*52.9))}};​​Grid[RComp,FrameAll]
Out[]=
Orbital
Radial
1s
0.00519812
-0.0189036rZ
3/2
Z
2s
0.000918907
-0.0189036rZ
3/2
Z
(2-0.0189036rZ)
2p
0.0000100289
-0.0094518rZ
r
5/2
Z
3s
0.0000370511
-0.0063012rZ
3/2
Z
(27-0.340265rZ+0.000714692
2
r
2
Z
)
3p
0.0000261991
-0.0063012rZ
3/2
Z
(0.113422rZ-0.000357346
2
r
2
Z
)
3d
4.18687×
-9
10
-0.0063012rZ
2
r
7/2
Z

Radial Plots

Let’s plot the radial probability density for a few of these orbitals. This, of course, corresponds to
2
R
n,l
(r)
. The cell below setups up the functions for the radial component of the wavefunction. We can copy & paste the functions above or we can use the definitions below.
In[]:=
A2Z[n_,l_,Z_]:=
3/2
Z
a0
(n-l-1)!
(n+l)!
2
2
n
​​RZ[n_,l_,Z_,r_]:=A2Z[n,l,Z]
-Zr/(na0)
l
2Zr
na0
LaguerreL(n-l-1),(2l+1),
2Zr
na0
//Simplify
For the hydrogen 1s orbital,
In[]:=
Plot 0.00519812 ^(-0.0189036 r Z) Z^(3/2) from r=0 to 500 for Z=1
Plot[Evaluate[(0.00519812*Z^(3/2))/E^(0.0189036*r*Z)/.{Z->1}],{r,0,500}]
Out[]=
Here’s the probability density for hydrogen s-orbitals.
In[]:=
Block[{a0=52.9,Z=1},​​Plot[{RZ[1,0,Z,r]^2,RZ[2,0,1,r]^2,RZ[3,0,1,r]^2},{r,0,500},PlotLabelStyle["Probability Density for s-Orbitals",Blue,Bold,16],​​PlotLegends{"1s","2s","3s"},AxesLabel{Style["r (pm)",Blue,Bold,14]}]]
Out[]=
1s
2s
3s
Here’s the probability density for hydrogen p-orbitals
In[]:=
Block[{a0=52.9,Z=1},​​Plot[{RZ[2,1,Z,r]^2,RZ[3,1,Z,r]^2,RZ[4,1,Z,r]^2},{r,0,800},PlotLabelStyle["Probability Density for p-Orbitals",Blue,Bold,16],​​PlotLegends{"2p","3p","4p"},AxesLabel{Style["r (pm)",Blue,Bold,14]},PlotRangeAll]]
Out[]=
2p
3p
4p
◼
  • Notice any difference between s- and p-orbital probability density?

    • Radial Distribution Function

    Here’s the Wolfram entry for the RDF:
    Now let’s plot the radial distribution function for several orbitals.
    ◼
  • Notice the different ranges along the x-axes. What conclusions do you draw from this?

    • Probability

    Here, again, we assume that our wavefunction is real; we’re not using the complex conjugate.
    ◼
  • Determine the probability of finding a hydrogen 1s-electron between 0 and 100 pm from the nucleus?
    • (The Block function ensures that the definition of a0 remains within this section)
    1
    .
    Determine the probability of finding a hydrogen 2s-electron between 0 and 100 pm.
    2
    .
    Determine the probability of finding a hydrogen 2p-electron between 0 and 100 pm.

    Average Distance

    Solution

    The operator for distance is multiplication by r.
    ◼
  • Now use Wolfram to enter the expectation value expression to determine the average electron distance for the 1s-orbital.
    • 1
    .
    Determine the average electron distance for the hydrogen 2s-orbital.
    2
    .
    Determine the average electron distance for the hydrogen 2p-orbital.

    Most Probable Distance

    ◼
  • How do we find a function maximum? How does it relate to derivatives?
    • ◼
  • What is the most probable distance for a hydrogen 1s-electron? (You may need to do this in multiple steps in Wolfram.)
    • Start with the derivative:
    1
    .
    Determine the most probable electron distance for the hydrogen 2s-orbital.
    2
    .
    Determine the most probable electron distance for the hydrogen 2p-orbital.
    Wolfram Cloud

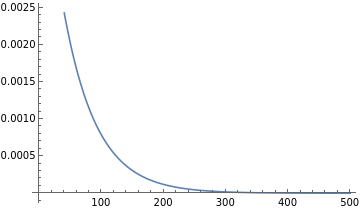
    You are using a browser not supported by the Wolfram Cloud

    Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


    I understand and wish to continue anyway »

    You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.