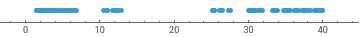Quick Foundation: Vector Spaces

Visualizing entities as points (represented by a list of numbers) in vector spaces

Single numbers (1D)

Simple case

Which numbers are closer to each other?
{1,6,8,19,7,21}
Let’s visualize them:
In[]:=
NumberLinePlot[{1,6,8,19,7,21}]
Out[]=

Let’s make it a little more complex ...

Which numbers are closer to each other?
In[]:=
numbers=
Out[]=
{2.91748,2.58475,38.8779,5.17159,35.4639,3.43902,12.8865,3.17415,30.7232,39.9808,39.5754,39.9336,3.13157,30.8344,5.904,2.96346,11.664,12.5453,36.7531,1.96803,12.0256,30.4299,5.15041,35.1926,33.2336,26.1885,27.2861,38.9637,36.3474,30.998,5.02725,36.4645,33.9447,39.7156,4.13711,37.2297,3.21325,35.4052,1.43734,10.9651,39.1853,12.2656,5.08272,36.2018,6.5651,6.61242,5.47358,37.2553,37.6554,35.002,4.90866,1.43139,35.7345,1.93139,26.3202,2.03956,2.64124,5.18829,38.4046,25.4629,30.1716,4.52939,25.4593,1.76716,5.09945,11.0365,25.325,26.545,5.72179,3.81483,6.53859,5.9974,38.1264,39.8559,6.94288,37.4593,3.37336,35.4115,4.87247,5.50739,33.561,11.1144,35.4453,30.2812,34.7469,27.5489,1.65906,2.58109,5.87168,37.6435,25.1506,6.5075,3.54959,31.3157,4.17196,2.33679,39.7293,6.00207,3.92181,33.6116,30.0097,36.6941,5.1776,30.5534,30.3552,39.353,31.4886,3.22308,12.2009,31.4406,3.46052,36.6111,6.55127,26.4293,10.5189,5.09798,39.3293,5.0461,31.9048,37.6677}
In[]:=
numbers//Column
Out[]=
2.91748
2.58475
38.8779
5.17159
35.4639
3.43902
12.8865
3.17415
30.7232
39.9808
39.5754
39.9336
3.13157
30.8344
5.904
2.96346
11.664
12.5453
36.7531
1.96803
12.0256
30.4299
5.15041
35.1926
33.2336
26.1885
27.2861
38.9637
36.3474
30.998
5.02725
36.4645
33.9447
39.7156
4.13711
37.2297
3.21325
35.4052
1.43734
10.9651
39.1853
12.2656
5.08272
36.2018
6.5651
6.61242
5.47358
37.2553
37.6554
35.002
4.90866
1.43139
35.7345
1.93139
26.3202
2.03956
2.64124
5.18829
38.4046
25.4629
30.1716
4.52939
25.4593
1.76716
5.09945
11.0365
25.325
26.545
5.72179
3.81483
6.53859
5.9974
38.1264
39.8559
6.94288
37.4593
3.37336
35.4115
4.87247
5.50739
33.561
11.1144
35.4453
30.2812
34.7469
27.5489
1.65906
2.58109
5.87168
37.6435
25.1506
6.5075
3.54959
31.3157
4.17196
2.33679
39.7293
6.00207
3.92181
33.6116
30.0097
36.6941
5.1776
30.5534
30.3552
39.353
31.4886
3.22308
12.2009
31.4406
3.46052
36.6111
6.55127
26.4293
10.5189
5.09798
39.3293
5.0461
31.9048
37.6677
Visualization helps:
In[]:=
NumberLinePlot[numbers]
Out[]=

Distance of one entity from another ...

Out[]=
What is the distance from one number to another?
In[]:=
EuclideanDistance[19,21]
Out[]=
2
In[]:=
EuclideanDistance[1,21]
Out[]=
20
Which number is further away from 21?

Pairs of numbers (2D)

Simple example

Let’s move to 2 dimensions.
Say something is represented by 2 numbers. Here are 4 such things:
How far are they from each other?

Can you think of something represented by 2 numbers?

Geographic coordinates: Latitude and Longitude

Similar idea as the first example with pairs of numbers

What problem can we solve with such numbers?

Triplets (3D)

Simple example

Let’s move to 3 dimensions.
Say something is represented by 3 numbers. Here are 10 such things:
How far are they from each other?

A single point

Can you think of something represented by 3 numbers?

What about digital representation of colors?

100 colors

N Dimensions

Movies in 3 dimensional feature space

If we were to represent movies in 3 dimensions (just like the colors) ...
Instead of Red, Green and Blue,
say we somehow measure genre of the content: Comedy, Sci Fi, Action

Movies in n-dimensional feature space

Instead of three, choose as many dimensions as you want.
◼
  • Comedy,
    • ◼
  • Tragedy,
    • ◼
  • Informative,
    • ◼
  • Action,
    • ◼
  • SciFi,
    • ◼
  • Romance,
    • ◼
  • Historic,
    • ◼
  • Apocalyptic, .....
    • ◼
  • Strong Female Protagonist, .....
    • ◼
  • Year in which it was created,
    • ◼
  • Won an Oscar,

    • People who watched and rated the movies in Feature Space