Klein-Nishina Formula for Compton Effect
Klein-Nishina Formula for Compton Effect
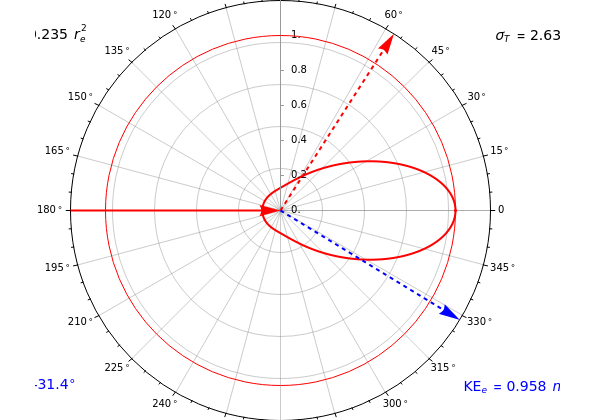
Low-energy (Thomson) scattering of a photon by an electron is approximated by the differential scattering cross section =(1+θ), where ==2.818×cm, the classical electron radius. The corresponding total scattering cross-section is given by =2πsinθdθ=. The Thomson formula is, however, inadequate to treat the higher-energy photoelectric and Compton effects. Klein and Nishina (1929) derived the scattering cross-section according to Dirac's relativistic theory of the electron: =f(,θ)+-θ, where and =hν/m, the incident photon energy in units of the electron rest energy (511 KeV/). The formulas pertain to the average of the two photon polarizations. A polar plot of the differential scattering cross section is shown in the graphic, with photon energy selectable in the range 0–10 MeV. The cross-section is expressed in units of ≈7.94×≈794barns, with a maximum value of ==1, as shown by the light red circle. The directions of the scattered photons are shown by a dashed red arrow, while the scattered electron (initially at rest) follows the dashed blue arrow. Numerical values are given for the photon differential and total cross sections, the electron scattering angle and the electron kinetic energy .
dσ
dΩ
1
2
2
cos
2
r
e
r
e
2
e
m
2
c
-13
10
σ
T
π
∫
0
dσ
dΩ
8π
3
2
r
e
dσ
dΩ
1
2
2
r
e
2
f(,θ)
E
γ
E
γ
-1
f(,θ)
E
γ
2
sin
f(,θ)=1[1+(1-cosθ)]
E
γ
E
γ
E
γ
2
c
2
c
2
r
e
-26
10
2
cm
dσ
dΩ
2
r
e
ϕ
e
KE
e
Details
Details
Snapshot 1: at low energies, the Klein–Nishina formula reduces to Thomson's formula, which is symmetrical for forward and backward scattering
Snapshot 2: as the energy increases, the differential cross section profile becomes less symmetrical
Snapshot 3: at higher energies, forward scattering predominates and the total cross section decreases with energy
Reference
Klein-Nishina Formula (Wikipedia).
External Links
External Links
Permanent Citation
Permanent Citation
S. M. Blinder
"Klein-Nishina Formula for Compton Effect"
http://demonstrations.wolfram.com/KleinNishinaFormulaForComptonEffect/
Wolfram Demonstrations Project
Published: December 3, 2009