Eigenvalues and the Principal Invariants of a Linear Map
Eigenvalues and the Principal Invariants of a Linear Map
The quantities =tr(A), =-tr(), =det(A) are called the principal invariants of the matrix .
I
1
I
2
1
2
2
tr(A)
2
A
I
3
A
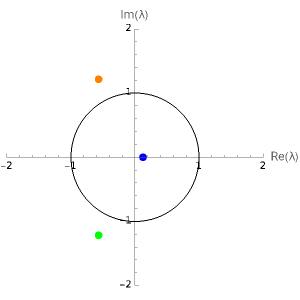
Drag the point in the - plane and move the slider to display the corresponding eigenvalues around the unit circle in the complex plane.
I
1
I
2
I
3
In the left-hand graphic, the discriminant is negative in the purple region; in the orange region, the eigenvalues have modulus less than one.
The eigenvalues of the matrix determine how the flow of a differential map or the orbit of a discrete map behaves.
A