Precision Error

k

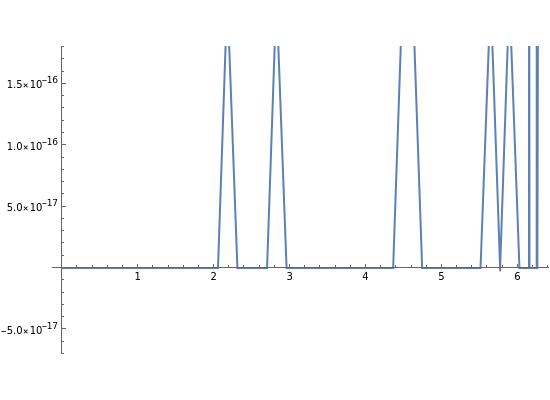
The plots in this Demonstration show precision error. The formula

arctan(x)+arctan(1/x)=π/2

is true for all real

x≠0

. To plot

arctan(kx)+arctan(1/(kx))-π/2

for various

k

, Mathematica correctly finds numerical values very close to 0. In the plot, these infinitesimal deviations are magnified a quadrillion-fold.

Various types of machine error—round-off, precision, accumulated—have led to the loss of lives and fortunes. For example, the Patriot missile system relies on a.1 second internal clock. The binary machine considers this as a 209715/2097152 second clock. In a 1991 incident during Operation Desert Storm, after being on for 100 hours, the missile tracking timing had accumulated a.34 second error. This rendered it unable to track an incoming missile, which subsequently fell intact on a barracks and killed 28 people.

Details

Patriot missile incident GAO report: http://www.fas.org/spp/starwars/gao/im92026.htm.

External Links

Error Propagation (Wolfram MathWorld)

Roundoff Error (Wolfram MathWorld)

Significant Digits (Wolfram MathWorld)

Permanent Citation

Ed Pegg Jr

"Precision Error"
http://demonstrations.wolfram.com/PrecisionError/
Wolfram Demonstrations Project
Published: January 25, 2008