Mackey-Glass Equation

maturation delay

15

plot type

x(t-τ) versus x(t)

solution time (days)

600

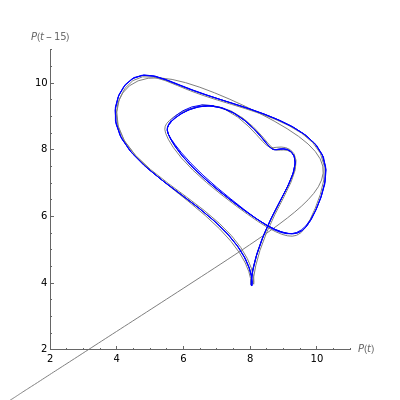
This Demonstration shows solutions of the Mackey–Glass equation

′

P

(t)

β

n

θ

x(t-τ)

n

P(t-τ)

+

n

θ

-γP(t)

for the density,

P

, of mature circulating white blood cells. The parameter

τ

is the delay between production and maturation and release into the bloodstream of the cells.

Details

The first half of the solution is shown in gray so that you can see how transients decay. The values of

β,θ,n

, and

γ

are constant and chosen to be the same as those shown in figure 2 of[1].

[1] M. C. Mackey and L. Glass, "Oscillation and Chaos in Physiological Control Systems," Science, 197, pp. 287–289.

Snapshot 1: with

τ=6

reproduces figure 2(b) in[1]

Snapshot 2: with

τ=20

reproduces figure 2(c) in[1]

Snapshot 3: the same value of

τ

as snapshot 2 in the delay plane

Snapshot 4: shows a very chaotic solution with

τ=25

Snapshot 5: there is an attractive fixed point

P=θ

with

τ=4.6

Snapshot 6: there is a limit cycle with

τ=4.8

External Links

Advanced Numerical Differential Equation Solving in (Wolfram Documentation Center)

Permanent Citation

Rob Knapp

"Mackey-Glass Equation"
http://demonstrations.wolfram.com/MackeyGlassEquation/
Wolfram Demonstrations Project
Published: March 7, 2011