Earthquake Focal Mechanism
Earthquake Focal Mechanism
This Demonstration generates earthquake focal mechanism plots, also called fault plane solution plots or simply beach balls. You can define the strike, dip, and rake angle of a fault and choose between different types of projections and focal hemispheres.
Details
Details
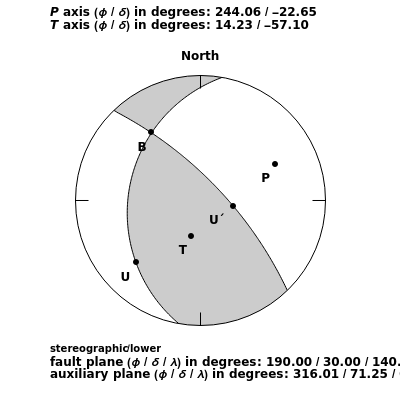
Earthquake focal mechanisms plots display the geometry of an earthquake fault, the direction of slip, and the deformation within the source region in a single diagram. This diagram, also called a beach ball plot by seismologists, is obtained by projecting the intersection of the fault plane and a perpendicular auxiliary plane with a selected hemisphere (upper or lower) of an imaginary spherical shell around the earthquake hypocenter. This imaginary sphere of unit radius is called the focal sphere.
The type of projection is commonly a stereographic or an equal area projection. Fault plane and auxiliary plane separate quadrants within the focal sphere that during the earthquake rupture have undergone different types of deformation. Those quadrants which in the projection correspond to white segments have undergone compression while those segments corresponding to the gray segments have undergone dilatation.
The projections of the directions of maximum compression and dilatation are labelled the axis and axis, respectively. U corresponds to the projection of the slip vector of the so-called hanging wall of the fault with respect to the foot wall. U´ corresponds to the direction of slip on the auxiliary plane that would produce the same spatial distribution of radiated seismic energy if the slip had occurred on the auxiliary plane. The B axis corresponds to the intersection of the fault plane and the auxiliary plane.
P
T
External Links
External Links
Permanent Citation
Permanent Citation
Frank Scherbaum, Nicolas Kuehn, Björn Zimmermann
"Earthquake Focal Mechanism"
http://demonstrations.wolfram.com/EarthquakeFocalMechanism/
Wolfram Demonstrations Project
Published: December 10, 2009