Driven Damped Simple Single Pendulum released from rest
Driven Damped Simple Single Pendulum released from rest
Description
Description
A simple pendulum is driven by an applied torque. What happens as you make the torque stronger?
The parameters we use are:
=3ω/2, where ω is the driving frequency and has been set equal to 2π for convenience.
β =/4 so that this system is underdamped.
γ is varied.
ω
0
β =
ω
0
γ is varied.
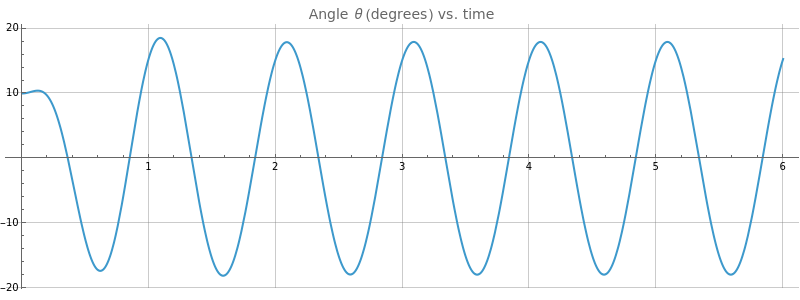
Angle and Angular Velocity vs time
Angle and Angular Velocity vs time
In[]:=
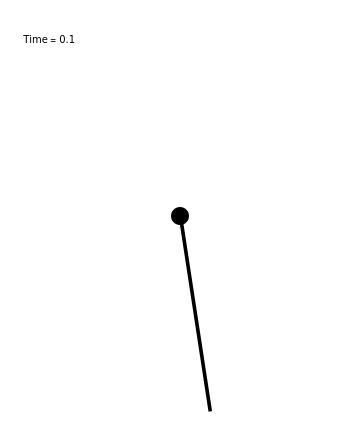
ManipulateModule{eq1,sol,p1},With{ω=2π},eq1=θ''[t]+2βθ'[t]+Sin[θ[t]]==γCos[ωt];sol=ParametricNDSolve[{eq1,θ[0]==θ0,θ'[0]==0},{θ,θ'},{t,0,tfinal},{β,ω0,γ,θ0}];Row@ColumnPlotθω,ω,γval,θ0val[t]/.sol,{t,0,tfinal},GridLines->Automatic,AspectRatio->13,PlotLabel->Row[{Style["Angle θ (degrees) vs. time",FontSize->14]}],ImageSize->{800,300},PlotRange->All,PlotPoints->100,Plotθ'ω,ω,γval,θ0val[t]/.sol,{t,0,tfinal},ImageSize->{800,100},AspectRatio->Full,PlotLabel->Style["Angular velocity vs. time",FontSize->14],PlotPoints->100,AnimateEvaluate@Graphics{PointSize[0.05],Point[{0,0}]},Thickness[.01],Line[{{0,0},{Sin[θ],-Cos[θ]}}]/.θ->θ,ω,γval,θ0val[t]/.sol/.t->tcurrent,{Text[Row[{"Time = ",tcurrent}],{-.8,0.9}]},PlotRange->{{-1.1,1.1},{-1.1,1.1}},AspectRatio->Full,{tcurrent,0.1,tfinal},AnimationRepetitions->1,AnimationRate->.5,{{γval,0.2,Style["Forcing Magnitude γ",FontSize->14]},0.01,1.2},{{tfinal,6,Style["Length of simulation",FontSize->14]},3,100,1},{{θ0val,10Degree,Style["Initial Angle",FontSize->14]},-90Degree,90Degree,5Degree}
2
ω0
2
ω0
1
Degree
3
2
4
3
2
3
2
4
3
2
θ
1.5ω
4
3
2
Out[]=
Cloud Deploy
Cloud Deploy
In[]:=
CloudPublish[]