Pendulum with Counterweight

​
pendulum
rod length
2.68
mass
1.45
initial angular position
1.328
counterweight
initial angular position
1.5708
hide trace of pendulum bob
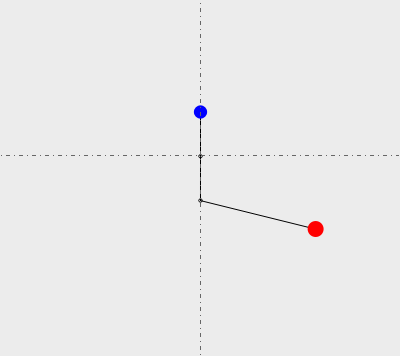
A rod is supported in the middle (which is taken as the origin) and can turn freely. On one end of the rod there is a pivot with a pendulum attached to a red bob swinging from it. At the other end of the rod is a blue counterweight.
Lagrangian mechanics is used to compute the equations of motion of the counterweight and the pendulum and to plot the trace of the pendulum bob.
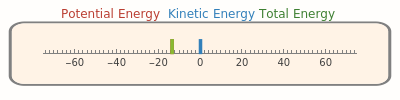
A horizontal energy gauge shows the total energy of the system, which remains constant as the potential and kinetic energy magnitudes change in opposite directions.

Details

The system as described has two degrees of freedom:
ϕ(t)
and
θ(t)
are the angular displacements of the counterweight arm and the pendulum, with initial values
ϕ
0
and
θ
0
.
The rod length is
1
and the counterweight has mass
1.
The pendulum has rod length
r
and its bob has mass
m
.
The potential energy of the system is
V=gsinϕ(t)-gm(rcosθ(t)+sinϕ(t))
.
The kinetic energy of the system is
T=
1
2
m
2
r
2
′
θ
(t)
-2r
′
θ
(t)
′
ϕ
(t)sin(θ(t)+ϕ(t))+
2
′
ϕ
(t)
+
1
2
2
′
ϕ
(t)
.
The resulting Lagrangian is
ℒ=T-V
and the equations of motion are
-gmcosϕ(t)+gcosϕ(t)-mr
′′
θ
(t)sin(θ(t)+ϕ(t))-mr
2
′
θ
(t)
cos(θ(t)+ϕ(t))+m
′′
ϕ
(t)+
′′
ϕ
(t)0
,
gsinθ(t)+r
′′
θ
(t)-
′′
ϕ
(t)sin(θ(t)+ϕ(t))+
2
′
ϕ
(t)
(-cos(θ(t)+ϕ(t)))0
.

Permanent Citation

Erik Mahieu
​
​"Pendulum with Counterweight"​
​http://demonstrations.wolfram.com/PendulumWithCounterweight/​
​Wolfram Demonstrations Project​
​Published: October 3, 2014