Charged Harmonic Oscillator in Electric Field
Charged Harmonic Oscillator in Electric Field
For an electron (mass , charge ) bound by a harmonic potential m and acted upon by a constant external electric field , the Schrödinger equation can be written as
m
-e
1
2
2
ω
2
x
E
-''(x)+m-eEx(x)=(x)
2
ℏ
2m
ψ
n
1
2
2
ω
2
x
ψ
n
E
n
ψ
n
An exact solution can be obtained by completing the square in the potential energy [1]:
V(x)=mx--=m-
1
2
2
2
ω
eE
m
2
ω
2
e
2
E
2m
2
ω
1
2
2
ω
2
ξ
2
e
2
E
2m
2
ω
Introducing the new variable , the Schrödinger equation can be written as
ξ=x-
eE
m
2
ω
-''(ξ)+m(ξ)=+(ξ)=n+ℏω(ξ)
2
ℏ
2m
Ψ
n
1
2
2
ω
2
ξ
Ψ
n
E
n
2
e
2
E
2m
2
ω
Ψ
n
1
2
Ψ
n
n=0,1,2,…
making use of the known solution of the standard harmonic-oscillator problem, expressed in terms of . The perturbed energies are shifted downward by a constant term:
ξ
E
n
1
2
2
e
2
E
2m
2
ω
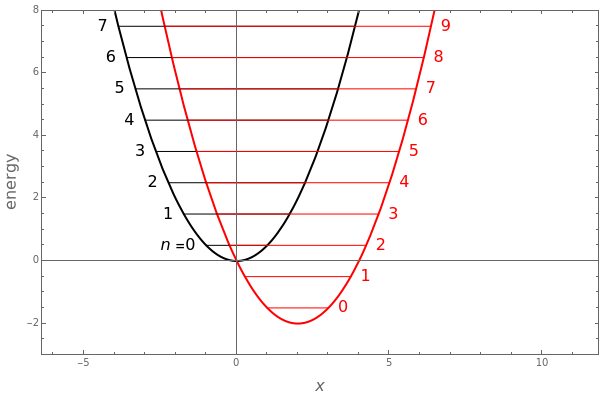
The graphic shows the potential energy and energy levels for the unperturbed (in black) and perturbed (in red) oscillator, for selected values of and . For simplicity, atomic units, , are used.
ω
E
ℏ=m=e=1
If the electric field is turned on during a time interval that is short compared to the oscillation period , the sudden approximation in perturbation theory can be applied [2]. Accordingly, the transition probability from state to a state is given by . These results can be seen by selecting "show transition probabilities" and the initial state .
Δt
2π/ω
n
m
P(nm)=
2
〈|〉
Ψ
m
ψ
n
n