Steady-State Two-Dimensional Convection-Diffusion Equation

Reynolds number

25

Prandtl number

1

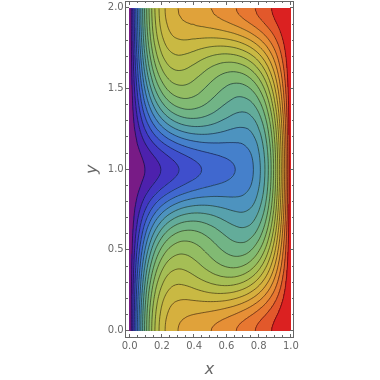
Consider the following two-dimensional convection-diffusion problem [1]:

1

PrRe

2

∂

T

∂

2

x

+

2

∂

T

∂

2

y

-u

∂T

∂x

-v

∂T

∂y

=0

,

where

T(0,y)=0

,

T(1,y)=1

,

0≤x≤L=1

, and

0≤y≤W=2

. Here,

Re

and

Pr

are the Reynolds and Prandtl numbers,

T(x,y)

is the unknown temperature distribution, and

(u,v)

is the given velocity field. Take

u=-sin(πx)cos(πy)

and

v=cos(πx)sin(πy)

; then the temperature

T(x,y)

is symmetric with respect to the

y=1

plane and the following Neumann conditions apply:

∂T

∂y

y=0

=

∂T

∂y

y=2

=0

.

This Demonstration uses the finite-element capabilities of Mathematica in order to readily compute the temperature distribution for user-set values of the dimensionless numbers,

Re

and

Pr

.

If you increase

Pr

, then you can observe that the temperature diffusion is much stronger. That is, the high temperatures generated at the right boundary penetrate much farther toward the left, which is the cold boundary.