Constrained Optimization

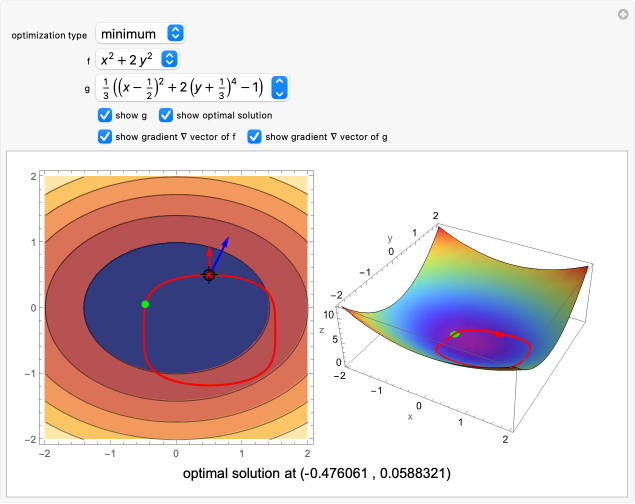
This Demonstration shows the minimization or maximization of a function

f

(blue) subject to a constraint

g=0

(red). The green point shows the optimal solution.

The graphic on the left shows the level curves of

f

and

g

together with the gradients. On the right, a 3D graphic of the function is shown together with the constraint of

g=0

projected onto the surface of

f

.

For either the minimum or maximum, the gradients of the function and the constraint are parallel:

∇f=λ∇g

, with the Lagrange multiplier

λ

. By moving the point around the plot region, you can see that this is a necessary condition for constrained optimization.

Edda Eich-Soellner