Classical Approximations of Pi

​
terms
method
Vieta
Wallis
Gregory
Euler
Euler variant
Machin
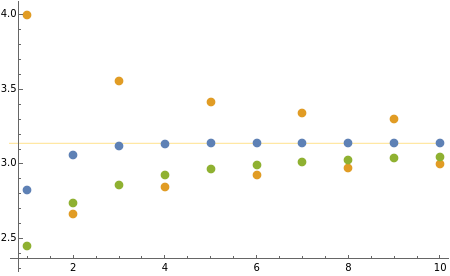
Since the discovery of
π
in antiquity, people have been fascinated with calculating its numerical value. Various infinite sums or products have been developed over the years. The success of such a method is determined by how fast it approaches its goal. This Demonstration compares several classical approximations for
π
and their rates of convergence.

Details

Here are the various methods used in this Demonstration:
​
Vieta's formula:
2
π
=
1
2
2
1
2
2+
2
1
2
2+
2+
2
…
Wallis's product:
2
π
=
3×3×5×5×7…
2×2×4×4×6×6…
Gregory series:
π
4
=
∞
∑
j=0
j
(-1)
2j+1
Euler's series:
2
π
6
=
∞
∑
j=1
1
2
j
Euler's series variant:
2
π
8
=
∞
∑
j=0
1
2
(2j+1)
Machin's arc tangent formula:
π=16
n
∑
j=0
j
(-1)
2j+1
2j+1
1
5
-4
n
∑
j=0
j
(-1)
2j+1
2j+1
1
239

External Links

Pi (Wolfram MathWorld)
Pi Formulas (Wolfram MathWorld)
Vieta's Formulas (Wolfram MathWorld)
Wallis Formula (Wolfram MathWorld)
Gregory Series (Wolfram MathWorld)
Machin's Formula (Wolfram MathWorld)

Permanent Citation

Rob Morris
​
​"Classical Approximations of Pi"​
​http://demonstrations.wolfram.com/ClassicalApproximationsOfPi/​
​Wolfram Demonstrations Project​
​Published: September 28, 2007