Random Walk Solutions to the Dirichlet Problem for the Laplace Equation
Random Walk Solutions to the Dirichlet Problem for the Laplace Equation
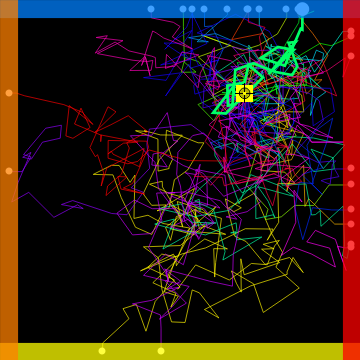
The Dirichlet problem seeks to find the solution to a partial differential equation inside a domain , with prescribed values on the boundary of . In 1944, Kakutani showed that the Dirichlet problem for the Laplace equation +=0 can be solved using random walks as follows. Given a point in the interior of , generate random walks that start at and end when they reach the boundary of . Then compute the average of the values of the given function at these boundary points. This average value is approximately equal to the value of the solution to the Dirichlet problem at the point .
D
D
f
xx
f
yy
P
D
P
D
P
This Demonstration illustrates this method in the case when the domain is a square and the function takes on prescribed values on each of the four sides. Choose boundary values and use the locator to select a point inside the square. The Demonstration then generates 20 random walks starting at and ending at the boundary of the square and computes the average value at the endpoints of these random walks. This is shown, along with the exact value of the solution at the point .
D
P
P
P
Details
Details
The random walks are generated using steps given by a two-dimensional normal distribution with standard deviation equal to the "scale" parameter. As the scale approaches 0, these random walks approach a Brownian motion starting at the point and ending at the boundary of , and the average value of the function at the endpoints of these random walks approaches the expected value of this stopped Brownian motion as the number of random walks approaches infinity. See[1].
P
D
References
References
[1] R. Hersh and R. J. Griego, "Brownian Motion and Potential Theory," Scientific American, 220(3), 1969 pp. 66–74. doi:10.1038/scientificamerican0369-66.
External Links
External Links
Permanent Citation
Permanent Citation
Cameron Nachreiner
"Random Walk Solutions to the Dirichlet Problem for the Laplace Equation"
http://demonstrations.wolfram.com/RandomWalkSolutionsToTheDirichletProblemForTheLaplaceEquatio/
Wolfram Demonstrations Project
Published: March 5, 2019