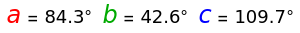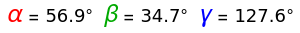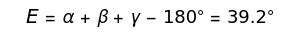Spherical Trigonometry on a Gnomonic Projection
Spherical Trigonometry on a Gnomonic Projection
A gnomonic projection is obtained by projecting points on the surface of a sphere from the sphere's center to a plane tangent to the sphere. In this Demonstration, the tangent point is taken as the North Pole, so that loci of constant are circles, while those of constant are radial spokes. This projection can be used to project slightly less than one hemisphere at a time onto a finite plane. The transformation equations are , . A gnomonic projection is neither conformal nor area-preserving, but has the distinctive feature that great circle arcs are mapped into straight lines. This suggests that it might be instructive to apply the gnomonic projection to spherical trigonometry.
θ
ϕ
ξ=tanθcosϕ
η=tanθsinϕ
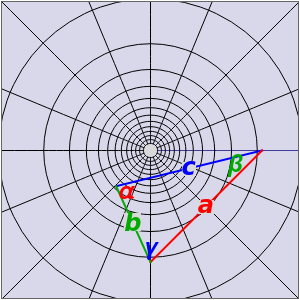
Spherical triangles with sides , , and angles , , , all expressed in degrees, are shown on a hemisphere and on a gnomonic projection. You can drag the vertices. The triangles conform to spherical analogs of the law of cosines, and also , with two other cyclic permutations for each. The spherical law of sines has the form . The sum of the angles of a spherical triangle is greater than 180°, and it is useful to define the spherical excess . The area enclosed by a triangle on the unit sphere, as well as the subtended solid angle, is equal to , expressed in steradians.
a
b
c
α
β
γ
cosa=cosbcosc+sinbsinccosα
cosα=-cosβcosγ+sinβsinγcosa
sinα/sina=sinβ/sinb=sinγ/sinc
E=α+β+γ-180°
E