Temperature Distribution in Four-Layer Skin Tissue

temperature along tissue depth

volumetric heat generation, W/

100

distance along tisssue length, m

heater length, % tissue length

50.

distance along tissue depth, m

0.01675

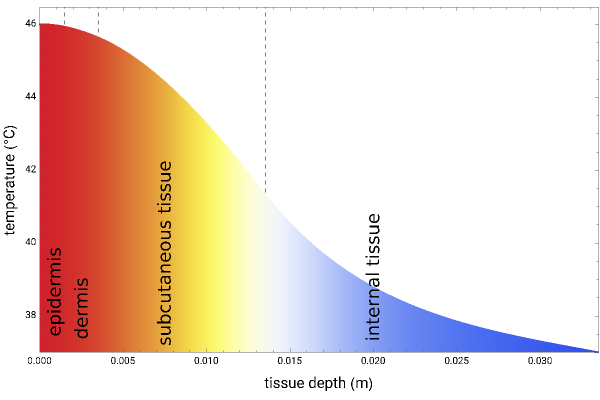
This Demonstration models the temperature distribution of four skin layers subjected to an external heat source. Human skin is modeled as a four-layer structure consisting of the epidermis, the dermis, the subcutaneous tissue and an internal tissue. Assume that each layer is homogeneous, and assume that blood perfusion, thermal conductivity and heat capacity are constant in each layer. Assume also that the layers are perfectly bonded to each other to enable a continuous flow of heat across the interfaces.

Details

Two-dimensional steady-state heat transfer in biological tissue is governed by the Pennes bioheat equation[1]:

∂

ωρ

(T-

ext

with boundary conditions:

∂T(0,y)

∂x

∂T(L,y)

∂x

∂T(x,0)

∂y

T(x,H)=

and

- q ext k e	L/2(1-f/100)≤x<L/2(1+f/100)
0	L/2(1+f)<x<L/2(1-f/100).

Here:

and

are the length and depth of the skin, respectively

is the length of the heating source expressed as a percent of the skin length

and

are the skin length and depth coordinates, respectively

and

represent the skin and blood temperatures, respectively

is the blood perfusion rate per unit volume

is the blood heat capacity

is the skin thermal conductivity

is the thermal conductivity of the epidermis

is the metabolic heat generation

ext

is the heat generation due to an external source

is an expression for the quantity of heat and the length of the heat source as a percent of the length of the skin

These equations are solved with the built-in Mathematica function NDSolve, using a different set of parameters

ωρ

ext

for each skin layer.

You can vary the intensity and length of the external heat source

and the location in the skin

and

to determine the temperature distribution of the skin tissue.

References

[1] F. Xu, T. J. Lu, K. A. Seffen and E. Y. K. Ng, "Mathematical Modeling of Skin Bioheat Transfer," Applied Mechanics Reviews, 62(5), 2009 050801. doi:10.1115/1.3124646.

Permanent Citation

Clay Gruesbeck

"Temperature Distribution in Four-Layer Skin Tissue" from the Wolfram Demonstrations Project http://demonstrations.wolfram.com/TemperatureDistributionInFourLayerSkinTissue/
Published: January 10, 2020