Floating Ball

radius (m)

5

specific gravity

0.3

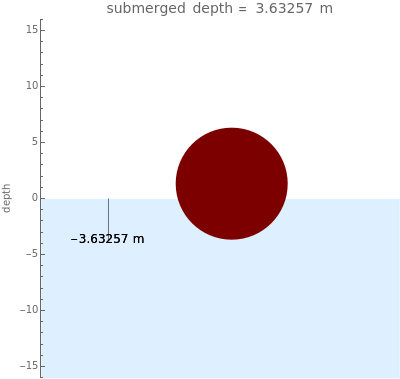
This Demonstration shows how far a floating spherical ball sinks into water by applying Archimedes's principle, calculus, and the solution of nonlinear equations.

Details

The solution runs as follows. Let

w

be the weight of the ball and

f

be the buoyancy force. Then

w=f

.

Let the volume of the ball be

V=

4

3

π

3

R

(where

R

is the radius),

ρ

b

be its density

kg

3

m

), and

g

be the acceleration due to gravity

(m/

2

s

).

The weight of the ball is given by the product of the volume, density, and

g

:

w=

4

3

π

3

R

ρ

b

g

The buoyancy force is given by the weight of water displaced, which is the product of the volume under water and the density of water

ρ

w

:

f=π

2

x

R-

x

3

ρ

w

g

,where

x

is the depth to which ball is submerged.

Therefore, with the specific gravity of the ball

γ

b

=

ρ

b

ρ

w

, we have

4

3

π

3

R

ρ

b

g=π

2

x

R-

x

3

ρ

w

g

, or

4

3

R

γ

b

-3

2

x

R+

3

x

=0

.

External Links

Equilibrium of a Floating Vessel

Learning Newton’s Method

Permanent Citation

Vincent Shatlock, Autar Kaw

"Floating Ball"
http://demonstrations.wolfram.com/FloatingBall/
Wolfram Demonstrations Project
Published: June 1, 2011