2. Writing a BrinkmanPDEComponent

BrinkmanPDEComponent
[vars,pars]
​ yields a porous media flow PDE term with variables vars and parameters pars.

Definition

The BrinkmanPDEComponent[vars,pars] function provides the symbolic structure of the Brinkman’s equation for porous media flow. This function can take one of two sets of parameters:
​
1. Dynamic Viscosity, Porosity, and Permeability, or
2. Reynolds Number and Darcy Number
​
The function is defined as follows:
In[]:=

Details

◼
  • BrinkmanPDEComponent models the flow of viscous fluids through porous media under applied constraints.
    • ◼
  • BrinkmanPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
    • BrinkmanPDEComponent[vars,...]〈boundarycondition〉
    ◼
  • BrinkmanPDEComponent creates PDE components for stationary parametric analysis.
    • ◼
  • BrinkmanPDEComponent models fluid flow phenomena with velocities
    u
    ,
    v
    and
    w
    in units of [
    m/s
    ] as dependent variables,
    x
    i
    ∈
    n
    
    as independent variables in units of [
    m
    ].
    • ◼
  • BrinkmanPDEComponent creates PDE components in two and three space dimensions
    • ◼
  • Stationary variables
    vars
    are
    vars={{u[
    x
    1
    ,…,
    x
    n
    ],v[
    x
    1
    ,…,
    x
    n
    ],…,p[
    x
    1
    ,…,
    x
    n
    ]},{
    x
    1
    ,…,
    x
    n
    }}
    .
    • ◼
  • BrinkmanPDEComponent creates a system of equations with the vector-valued Brinkman’s momentum equation combined with the continuity equation.
    • ◼
  • The equation of the model BrinkmanPDEComponent with dynamic viscosity μ [s Pa], porosity ϕ, and permeability κ
    [
    2
    m
    ]
    is based on the Brinkman’s momentum equation and the continuity equation:
    • μ
    κ
    V+∇·-
    μ
    ϕ
    (∇V)+∇p
    =
    0
    ∇·V
    =
    0
    ◼
  • The Reynolds number
    ℛℯ
    is defined as ℛℯ = ρ
    U
    L/μ, where
    L
    [
    m
    ] is a characteristic length and
    U
    the flow velocity.
    • ◼
  • The Darcy number  is defined as
    =κ
    2
    ϕL
    , where
    L
    [
    m
    ] is a characteristic length, κ
    [
    2
    m
    ]
    is the permeability, and ϕ is the porosity.
    • ◼
  • The following parameters pars can be given:
    • parameter
    default
    symbol
    "DynamicViscosity"
    -
    μ
    , dynamic viscosity [
    sPa
    ]
    "Porosity"
    -
    ϕ
    , porosity
    "Permeability"
    -
    κ
    , permeability
    [
    2
    m
    ]
    "ReynoldsNumber"
    -
    ℛℯ
    , Reynolds number
    "DarcyNumber"
    -
    ,Darcynumber
    ◼
  • Dimensionless form of the Brinkman’s equations can be obtained by making the substitutions
    *
    V
    =V/ϕU
    ,
    *
    p
    =p/ρ
    2
    U
    , and
    *
    x
    =x/L
    :
    • 1
    ℛℯ
    V+∇·-
    1
    ℛℯ
    (∇V)+∇p
    =0
    ∇·V
    =0
    ◼
  • Instead of material parameters, a Reynolds number
    ℛℯ
    and a Darcy number  can be specified.
    • ◼
  • BrinkmanPDEComponent uses
    "SIBase"
    units. The geometry has to be in the same units as the PDE.

    • Examples

    Basic Examples

    Define flow PDE through a porous medium:
    In[]:=
    BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"DynamicViscosity"->μ,"Porosity"->ϕ,"Permeability"->κ|>]//MatrixForm
    Out[]//MatrixForm=
    10000u[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    u[x,y])+
    (1,0)
    p
    [x,y]
    10000v[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    v[x,y])+
    (0,1)
    p
    [x,y]
    (0,1)
    v
    [x,y]+
    (1,0)
    u
    [x,y]
    Define stationary flow PDE model through porous medium with Reynolds number of 10 and Darcy number of
    -4
    10
    :
    In[]:=
    BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"ReynoldsNumber"->10,"DarcyNumber"->
    -4
    10
    |>]//MatrixForm
    Out[]//MatrixForm=
    1000u[x,y]+
    ∇
    {x,y}
    ·-
    1
    10
    ∇
    {x,y}
    u[x,y]+
    (1,0)
    p
    [x,y]
    1000v[x,y]+
    ∇
    {x,y}
    ·-
    1
    10
    ∇
    {x,y}
    v[x,y]+
    (0,1)
    p
    [x,y]
    (0,1)
    v
    [x,y]+
    (1,0)
    u
    [x,y]

    Scope

    Specify a flow PDE through porous medium with dynamic viscosity of
    -3
    10
    , porosity of 0.4, and permeability of
    -7
    10
    :
    In[]:=
    BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"DynamicViscosity"->
    -3
    10
    ,"Porosity"->0.4,"Permeability"->
    -7
    10
    |>]//MatrixForm
    Out[]//MatrixForm=
    10000u[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    u[x,y])+
    (1,0)
    p
    [x,y]
    10000v[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    v[x,y])+
    (0,1)
    p
    [x,y]
    (0,1)
    v
    [x,y]+
    (1,0)
    u
    [x,y]
    Activate a flow PDE through porous medium with Reynolds number of 0.5 and Darcy number of
    -2
    10
    :
    In[]:=
    Activate[BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"ReynoldsNumber"->0.5,"DarcyNumber"->
    -2
    10
    |>]]
    Out[]=
    200.u[x,y]-2.
    (0,2)
    u
    [x,y]+
    (1,0)
    p
    [x,y]-2.
    (2,0)
    u
    [x,y],200.v[x,y]+
    (0,1)
    p
    [x,y]-2.
    (0,2)
    v
    [x,y]-2.
    (2,0)
    v
    [x,y],
    (0,1)
    v
    [x,y]+
    (1,0)
    u
    [x,y]
    Specify a symbolic stationary flow PDE through porous medium in two dimensions with dynamic viscosity μ, porosity ϕ, and permeability κ:
    In[]:=
    BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"DynamicViscosity"->μ,"Porosity"->ϕ,"Permeability"->κ|>]
    Out[]=
    10000u[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    u[x,y])+
    (1,0)
    p
    [x,y],10000v[x,y]+
    ∇
    {x,y}
    ·(-0.0025
    ∇
    {x,y}
    v[x,y])+
    (0,1)
    p
    [x,y],
    (0,1)
    v
    [x,y]+
    (1,0)
    u
    [x,y]
    Specify a symbolic stationary flow PDE through porous medium in three dimensions with dynamic viscosity μ, porosity ϕ, and permeability κ:
    In[]:=
    BrinkmanPDEComponent[{{u[x,y,z],v[x,y,z],w[x,y,z],p[x,y,z]},{x,y,z}},<|"DynamicViscosity"->μ,"Porosity"->ϕ,"Permeability"->κ|>]
    Out[]=
    10000u[x,y,z]+
    ∇
    {x,y,z}
    ·(-0.0025
    ∇
    {x,y,z}
    u[x,y,z])+
    (1,0,0)
    p
    [x,y,z],10000v[x,y,z]+
    ∇
    {x,y,z}
    ·(-0.0025
    ∇
    {x,y,z}
    v[x,y,z])+
    (0,1,0)
    p
    [x,y,z],10000w[x,y,z]+
    ∇
    {x,y,z}
    ·(-0.0025
    ∇
    {x,y,z}
    w[x,y,z])+
    (0,0,1)
    p
    [x,y,z],
    (0,0,1)
    w
    [x,y,z]+
    (0,1,0)
    v
    [x,y,z]+
    (1,0,0)
    u
    [x,y,z]

    Applications

    Stationary Analysis

    Solve for the velocity and pressure in a porous cavity with antiparallel flow and a source term:
    In[]:=
    source={If[0.4<=x<=0.6&&0.4<=y<=0.6,100,0],0,0};​​{uVel,vVel,pressure}=NDSolveValue[​​{BrinkmanPDEComponent[{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"ReynoldsNumber"->0.5,"DarcyNumber"->
    -2
    10
    |>]+source=={0,0,0},​​DirichletCondition[{u[x,y]==1,v[x,y]==0},y==1],​​DirichletCondition[{u[x,y]==0,v[x,y]==0},0<y<1],​​DirichletCondition[{u[x,y]==-1,v[x,y]==0},y==0],​​DirichletCondition[p[x,y]==0,x==0&&y==0]},​​{u[x,y],v[x,y],p[x,y]},​​{x,y}∈Rectangle[{0,0},{1,1}],​​Method->{"FiniteElement","InterpolationOrder"->{u->2,v->2,p->1}}];
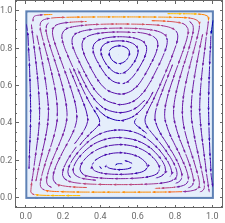
    Visualize the velocity of the fluid:
    In[]:=
    StreamPlot[{uVel,vVel},{x,y}∈Rectangle[{0,0},{1,1}]]
    Out[]=