Rational Pedal-Antipedal Triangles

x

1

y

1

z

2

u

-

1

3

v

7

6

rational pedal

rational antipedal

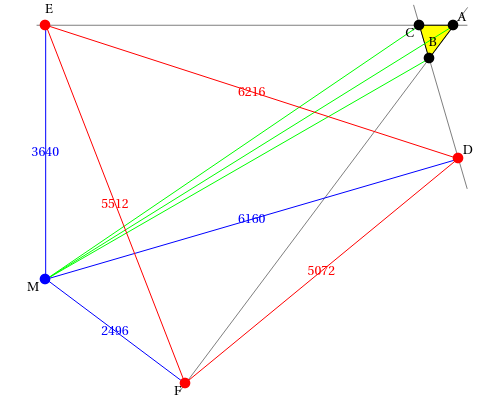
In a rational polygon, the distance between any two vertices is a rational number.

Let

DEF

be the pedal triangle or the antipedal triangle of any point

M

with respect to the triangle

ABC

.

A theorem states that

MABC

is a rational quadrilateral if and only if

MDEF

is a rational quadrilateral.

In this Demonstration, rational values

x

,

y

,

z

,

u

and

v

are used to generate a pair of rational pedal-antipedal triangles

ABC

and

DEF

that correspond to the rational point

M

.

External Links

Basic Parameters of the Second Fermat Point

Rational Isogonal Conjugates

Constructing a Rational Rectangle

Rational Cyclic Polygons

Seven Points with Integral Distances

Lengths of Sides and Angle Bisectors Are Rational Together

Integer Triangle of the Gergonne Point

Pedal Triangle (Wolfram MathWorld)

Antipedal Triangle (Wolfram MathWorld)

Rational Cyclic Orthodiagonal Quadrilateral

Rational Tangential Complete Quadrilateral

Permanent Citation

Minh Trinh Xuan

"Rational Pedal-Antipedal Triangles"
http://demonstrations.wolfram.com/RationalPedalAntipedalTriangles/
Wolfram Demonstrations Project
Published: March 17, 2023