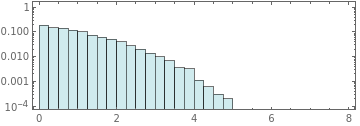
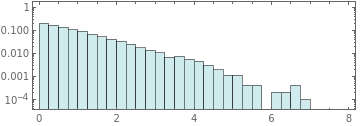
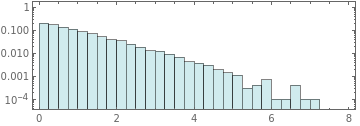
With[{data=NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​ConstantArray[1,1000],2000]},​​Histogram[Catenate[Take[data,-500]],​​Automatic,{"Log","Count"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->All,FrameTrue,AspectRatio1/3​​]]

Evolution

In[]:=
With[{data=NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​ConstantArray[1,10000],20]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTrue,AspectRatio1/3​​]&/@data]
Out[]=

,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,

In[]:=
GraphicsGrid[Partition[With[{data=NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​ConstantArray[1,10000],16]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTicks->None,FrameTrue,AspectRatio1/3​​]&/@data],4]]
Out[]=
In[]:=
8/30.
Out[]=
0.266667
In[]:=
GraphicsGrid[Partition[With[{data=NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​ConstantArray[1,10000],16]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTicks->None,FrameTrue,AspectRatio1/3​​]&/@data],4]]
Out[]=
In[]:=
GraphicsGrid[Partition[With[{data=NestList[EnergyExchangeAll[​​FixedEnergyExchange[True]],​​ConstantArray[1,10000],16]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTicks->None,FrameTrue,AspectRatio1/3​​]&/@data],4]]
Out[]=
In[]:=
GraphicsGrid[Partition[With[{data=NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​CenterArray[ConstantArray[100,100],10000],16]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTicks->None,FrameTrue,AspectRatio1/3​​]&/@data],4]]
Out[]=
In[]:=
GraphicsGrid[Partition[With[{data=Take[NestList[EnergyExchangeAllNN[​​FixedEnergyExchange[True]],​​CenterArray[ConstantArray[100,100],10000],1600],1;;-1;;100]},​​Histogram[#,{.25},{"Log","Probability"},​​ChartStyle$SecondLawColors["Blues",3],​​PlotRange->{{0,8},{Automatic,1}},FrameTicks->None,FrameTrue,AspectRatio1/3​​]&/@data],4]]
General
:4.5651×
-308
10
0.295132 is too small to represent as a normalized machine number; precision may be lost.
General
:1.31087×
-307
10
0.0193446 is too small to represent as a normalized machine number; precision may be lost.
General
:2.48449×
-308
10
0.0170639 is too small to represent as a normalized machine number; precision may be lost.
General
:Further output of General::munfl will be suppressed during this calculation.
Out[]=

Integer case

Fixed energy distribution fractions

One collision at a time...
[[[ Pure diffusion equation in energy space ]]]
Pure diffusion should approach uniform distribution.... [ others might be bimodal uniform ]
Weighted Pascal’s triangle.... [ but with wrapping ]

Initially uniform

Random Connections

Actual hard spheres