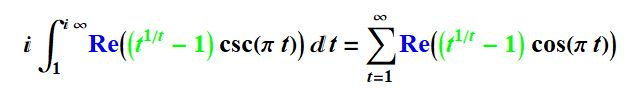Wolfram Cloud Document

Prove

2

/

2

This equation involves a complex integral and a series. To prove it, we need to delve into the realm of complex analysis, particularly focusing on techniques like contour integration and residue calculus.

Steps to Prove the Equality

1. Understand the Components:

• The left-hand side is an integral over the real part of a complex expression, multiplied by

csc(πt)

.

• The right-hand side is an infinite series over the real part of a similar expression, multiplied by

cos(πt)

.

2. Contour Integration:

• Consider the function

f(t)(

1/t

t

-1)csc(πt)

.

• Apply contour integration in the complex plane to evaluate the integral, making use of the properties of the complex exponential and trigonometric identities.

3. Residues and Poles:

• Identify the poles of the function within the contour and calculate the residues.

• Use the residue theorem to evaluate the contour integral, which relates the integral over the contour to the sum of residues inside the contour.

4. Relate Integral to Series:

• The integral can be transformed into a sum using residue calculus.

• The transformation will involve equating the integral over a part of the contour to the series over the residues, which leads to the series on the right-hand side.

5. Real Part Extraction:

• Since the integral and sum involve the real part, ensure that each step respects the real part extraction.

• Use symmetry and periodicity properties of trigonometric functions to simplify expressions.

6. Verification:

• Verify the equality by comparing terms on both sides, ensuring that each term in the series corresponds to the evaluation of a contour integral segment.

This is a sketch of the approach. Each step involves detailed calculations and logical deductions based on complex analysis principles. To fully carry out this proof, it would typically be done in a structured mathematical paper or detailed derivation. If you want to explore specific parts of the calculation or need mathematical software assistance, I can help with that as well.

How can the integral can be transformed into a sum using residue calculus?

To transform the integral into a sum using residue calculus, we can apply the residue theorem, which is a powerful tool in complex analysis. The key idea is to evaluate a contour integral around a closed path in the complex plane, which is related to the sum of the residues of the function within that contour. Here's a high-level outline of the process:

Steps to Transform the Integral into a Series

1. Identify the Function and Contour:

• Consider the function

.

• We want to evaluate an integral of the form

.

2. Extend the Function to the Complex Plane:

• Extend the function

to the complex plane, ensuring it is meromorphic (holomorphic except at isolated poles) within the region of interest.

3. Choose an Appropriate Contour:

• Construct a contour in the complex plane that includes the real line segment from 1 to

and a semicircular arc in the upper half-plane returning to the real line.

• The contour integral around this path can be decomposed into an integral over the real segment plus an integral over the arc.

4. Apply the Residue Theorem:

• The residue theorem states that the integral of a meromorphic function over a closed contour is

times the sum of the residues at the poles inside the contour.

• Identify the poles of the function

within the contour, particularly focusing on the poles introduced by

, which occur at

for

.

5. Calculate Residues:

• Calculate the residues of the function at each pole inside the contour. The residue at a simple pole

is given by:

6. Relate the Integral to the Series:

• The contour integral is equal to

times the sum of these residues.

• The integral along the semicircular arc should vanish as the radius goes to infinity if the function decreases sufficiently fast, leaving only the integral along the real line.

• This results in the transformation of the original integral into a sum over the residues, which corresponds to the series on the right-hand side.

By following these steps, the integral is effectively transformed into a sum using residue calculus. Each term in the series corresponds to a residue of the function at one of its poles. This powerful method leverages the properties of analytic functions and complex integration to evaluate difficult real integrals.

Do up to step 3.

Let's go through steps 1 to 3 in detail to set up the transformation of the integral using residue calculus.

Step 1: Identify the Function and Contour

We are given the integral:

To use residue calculus, we need to extend this to a complex function. The function under consideration is:

Step 2: Extend the Function to the Complex Plane

The expression

can be extended to the complex plane as

, where

is the complex logarithm. The function

is meromorphic in the complex plane with simple poles at integer values of

.Thus, the extended function is:

Step 3: Choose an Appropriate Contour

To apply residue calculus, we need to integrate over a closed contour. A typical contour for integrals from 1 to infinity is:1. The Line Segment: From

to

on the real axis, where

.2. The Semicircular Arc: A semicircle in the upper half-plane with radius

, connecting

back to

.This contour is denoted as

, which is the combination of the line segment and the semicircular arc.

Key Considerations for the Contour:

• Orientation: The contour should be traversed in the counterclockwise direction.

• Behavior of the Function: For

, the integral over the arc should vanish if the function

decreases fast enough as

.

By setting up this contour, we can apply the residue theorem, which states that the integral of a meromorphic function around a closed contour is

times the sum of the residues inside the contour. Now, with the contour set up, the next steps would involve identifying the poles inside this contour and calculating their residues. Let me know if you would like to proceed with these calculations or have any specific questions about the process so far.

identify the poles inside this contour and calculating their residues

To identify the poles and calculate the residues for the function

, we need to consider the poles introduced by the component functions.

Poles of the Function

1. **Poles of

:**

• The function

has simple poles at integer values of

, i.e.,

where

.

• Within the chosen contour, which includes the line from 1 to

and returns along a semicircular arc in the upper half-plane, the poles at

are inside the contour for sufficiently large

.

2. **Behavior of

:**

• This part of the function does not introduce additional poles. It is entire except for the branch cut of the logarithm, which does not affect the poles caused by

.

Calculating the Residues

The residues for the poles of a function at simple poles can be calculated using:

For each integer pole

:1. **Residue at

:**

• Consider

.

• Near

,

behaves like

, so:

• Simplified:

Since this expression can be complex, the real part affects the integral. Each term in the series corresponds to evaluating this residue at each integer

.

Next Steps

1. Sum the Residues:

• The sum of these residues multiplied by

gives the value of the contour integral.

2. Transform Back to the Real Line:

• The result of the contour integral should match the original integral over the real segment, transformed into a sum of residues.

This approach helps in comparing the integral to the desired series. Let me know if you'd like further assistance with specific calculations or verifying this process numerically or symbolically.

Do the next steps.