Swing the Logarithmic Curve around (1, 0)

​
base
2
The logarithmic function to the base
b
, where
b>0
and
b≠1
, is defined by
y=
log
b
x
if and only if
x=
y
b
; the domain is
0<x<∞
and the range is
-∞<y<∞
.
Move the slider; the base of the logarithm changes and you see its graph swing around the point
(1,0)
.
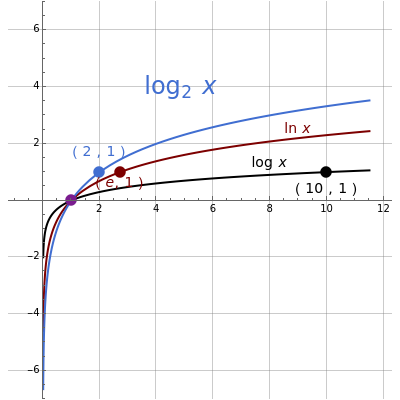
Closely observe the two cases
0<b<1
and
b>1
. Also notice where the blue curve lies in relation to the common logarithm
log
(base 10) and the natural logarithm
ln
.

Details

When considering the common logarithm (i.e., base 10), we notice that as the
x
values decrease from 1 to 0, the curve falls rapidly, and for
x0
, it approaches the negative
y
axis asymptotically. As the
x
values increase from 1 to 10, the function increases monotonically from 0 to 1, and as
x
values increase by a factor of 10 (for example, from 10 to 100) the function increases from 1 to 2. The same applies for the intervals
100≤x≤1000
,
1000≤x≤10000
, and so on. Because the changes are very small for such large intervals, the curve can be well approximated by a straight line.
To switch bases, we let
log
a
x=m
; we will show that
log
a
x=
log
b
x
log
b
a
.
By definition,
log
a
x=m
implies
x=
m
a
.
Taking the
log
to the base
b
of both sides gives
log
b
x=
log
b
m
a
=m
log
b
a
.
Dividing by
log
b
a
gives
m=
log
b
x
log
b
a
. Replacing
m
by
log
a
x
yields
log
a
x=
log
b
x
log
b
a
.

External Links

Logarithm (Wolfram MathWorld)
Rules for Logarithms
Geometry of Logarithms
Calculating Integer Logarithms in Different Bases
A Visualization of Logarithms

Permanent Citation

Abraham Gadalla
​
​"Swing the Logarithmic Curve around (1, 0)"​
​http://demonstrations.wolfram.com/SwingTheLogarithmicCurveAround10/​
​Wolfram Demonstrations Project​
​Published: March 7, 2011