Logistic Model for Population Growth

P

0

100

r

0.08

K

1000

t

0

dP

dt

= r P(1-

P

K

P(t) =

K

A

-r t

e

+ 1

, A =

K-

P

0

P

0

Play the animation for consistent time steps.

exact

P

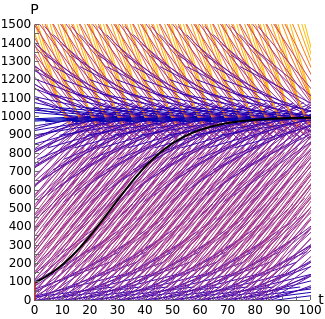
This Demonstration illustrates logistic population growth with graphs and a visual representation of the population. As time progresses, note the increase in the number of dots and how the rate of change increases but later decreases. Play the animation for

t

to see the behavior most clearly with discrete time steps. Compare this to exponential growth, presented in an analogous way in a companion Demonstration.

Details

The logistic model for population as a function of time

P(t)

is based on the differential equation

dP

dt

=rP1-

P

K

, where you can vary

r

and

K

, which describe the intrinsic rate of growth and the effects of environmental restraints, respectively. The solution of the logistic equation is given by

P(t)=

K

A

-rt

e

+1

, where

A=

K-

P

0

P