Collatz Sequences for ♯(n)
Collatz Sequences for
♯(n)
Paul Abbott
Collatz
Collatz
The Collatz sequence for can be computed as a fixed-point list of the “shortcut” Collatz map:
n
In[]:=
Collatz[n_]:=Collatz[n]=FixedPointListxIfOddQ[x],,,n,SameTest(mm2)
3x+1
2
x
2
Primorial
Primorial
The primorial is defined as the product of first prime numbers:
♯(n)
n
In[]:=
♯(n_):=
n
∏
k=1
p
k
Compute for :
♯(n)
1≤n≤10
In[]:=
♯/@Range[10]
Out[]=
{2,6,30,210,2310,30030,510510,9699690,223092870,6469693230}
By construction, each primorial is divisible by only one power .
2
Visualization
Visualization
Compute the sequence length for versus for :
♯(n)
log(♯(n))
1≤n≤1000
In[]:=
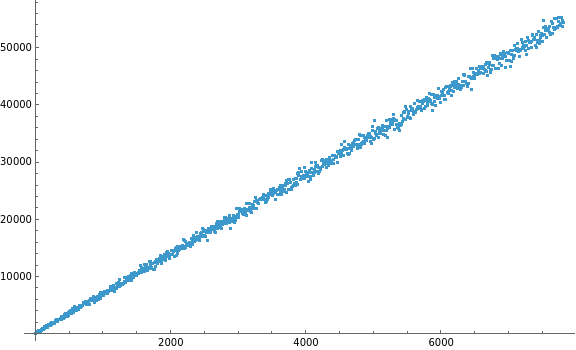
data=(n{Log[♯[n]],Length@Collatz[♯[n]]})/@Range[1000];
Display the data:
In[]:=
lp=ListPlot[data]
Out[]=
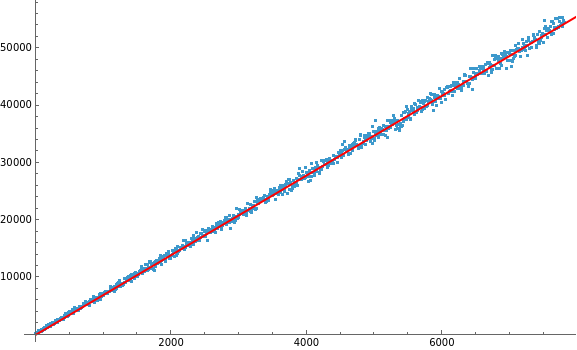
A linear fit works well:
In[]:=
fit=Fit[data,x,x]
Out[]=
6.95456x
In[]:=
Show[lp,Plot[fit,{x,0,},PlotStyle->Red]]
4
10
Out[]=