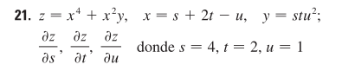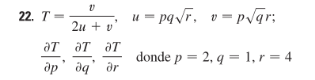In[]:=
(*Definicióndelasvariables*)ClearAll[z,x,y,s,t,u]​​​​x[s_,t_,u_]:=s+2t-u​​y[s_,t_,u_]:=stu^2​​z[s_,t_,u_]:=x[s,t,u]^4+x[s,t,u]^2*y[s,t,u]​​​​(*Derivadasparciales*)​​dzds=D[z[s,t,u],s];​​dzdt=D[z[s,t,u],t];​​dzdu=D[z[s,t,u],u];​​​​(*Mostrarlasderivadas*)​​dzds​​dzdt​​dzdu​​​​(*Evaluaciónenelpuntodado:s=4,t=2,u=1*)​​dzds/.{s->4,t->2,u->1}​​dzdt/.{s->4,t->2,u->1}​​dzdu/.{s->4,t->2,u->1}​​
Out[]=
4
3
(s+2t-u)
+2st(s+2t-u)
2
u
+t
2
(s+2t-u)
2
u
Out[]=
8
3
(s+2t-u)
+4st(s+2t-u)
2
u
+s
2
(s+2t-u)
2
u
Out[]=
-4
3
(s+2t-u)
+2st
2
(s+2t-u)
u-2st(s+2t-u)
2
u
Out[]=
1582
Out[]=
3164
Out[]=
-700
​
In[]:=
(*Definicióndelasvariables*)ClearAll[T,u,v,p,q,r];​​​​u[p_,q_,r_]:=p*q*Sqrt[r];​​v[p_,q_,r_]:=p*Sqrt[q]r;​​T[p_,q_,r_]:=v[p,q,r]/(2*u[p,q,r]+v[p,q,r]);​​​​(*Derivadasparciales(puedesdejarD[...]osimplificar)*)​​dTdp=D[T[p,q,r],p];​​dTdq=D[T[p,q,r],q];​​dTdr=D[T[p,q,r],r];​​​​(*Mostrarderivadassimbólicas*)​​dTdp​​dTdq​​dTdr​​​​(*Evaluaciónenelpuntodado:p=2,q=1,r=4*)​​pt={p->2,q->1,r->4};​​​​Print["El valor de ∂T/∂p en (2,1,4) es: ",dTdp/.pt];​​Print["El valor de ∂T/∂q en (2,1,4) es: ",dTdq/.pt];​​Print["El valor de ∂T/∂r en (2,1,4) es: ",dTdr/.pt];​​
Out[]=
-
p
q
r2q
r
+
q
r
2
2pq
r
+p
q
r
+
q
r
2pq
r
+p
q
r
Out[]=
-
p
q
r2p
r
+
pr
2
q
2
2pq
r
+p
q
r
+
pr
2
q
2pq
r
+p
q
r
Out[]=
-
p
q
p
q
+
pq
r
r
2
2pq
r
+p
q
r
+
p
q
2pq
r
+p
q
r
El valor de ∂T/∂p en (2,1,4) es: 0
El valor de ∂T/∂q en (2,1,4) es: -
1
8
El valor de ∂T/∂r en (2,1,4) es:
1
32
​
​
​
​