Runge's Phenomenon

number of points

5

sampling method

equally spaced

Chebyshev points

Chebyshev sample points

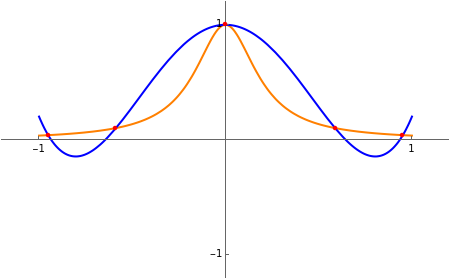
Runge's phenomenon illustrates the error that can occur when constructing a polynomial interpolant of high degree. The function to be interpolated,

y=

1

1+25

2

x

, is shown in orange, the interpolating polynomial in blue, and the data points in red. The difference between the interpolant and the function is shown below.

Details

Runge's function is given by

f(x)=

1

1+25

2

x

. When this function is sampled at equally spaced points in the range

x∈[-1,1]

, as the number of sample points increase the error difference theinterpolating polynomial and the function grow without bound. When Cheybshev points are used the error diminishes as the number of points increases.

External Links

Interpolation (Wolfram MathWorld)

Polynomial Degree (Wolfram MathWorld)

Lagrange Interpolating Polynomial (Wolfram MathWorld)

InterpolatingPolynomial (Wolfram Documentation Center)

Permanent Citation

Chris Maes

"Runge's Phenomenon"
http://demonstrations.wolfram.com/RungesPhenomenon/
Wolfram Demonstrations Project
Published: April 28, 2007