Joukowski Airfoil: Aerodynamic Properties
Joukowski Airfoil: Aerodynamic Properties
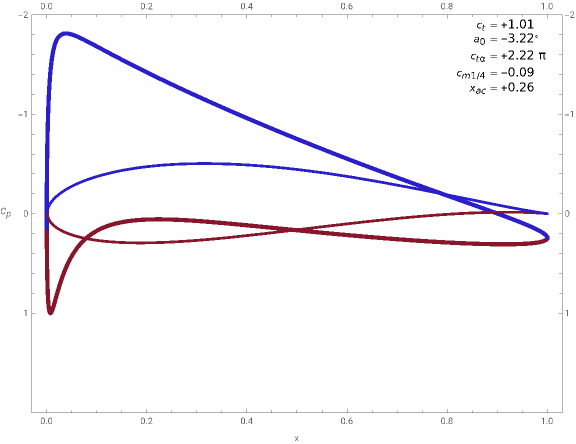
The surface pressure distribution for potential flow over one of the Joukowski family of airfoils is presented in the format conventional for airfoil aerodynamics; the characteristic length is the chord of the airfoil and pressure is presented as a dimensionless pressure coefficient. The shape of the airfoil is included as an insert. Slider controls are provided for the shape of the airfoil and the angle of attack.
For typical conditions, the upper part of the curve corresponds to the upper surface of the airfoil and the lower curve to the lower surface; color-coding is used to associate a part of the airfoil with the appropriate part of the pressure distribution. The area enclosed by the surface pressure coefficient curve is an estimate of the two-dimensional lift coefficient. Blasius's equations are used to compute lift and pitching moment characteristics, which are summarized by lift coefficient, angle of attack at zero lift, slope of lift coefficient curve, pitching moment about the quarter-chord and location of the aerodynamic center.
Details
Details
Details of potential flow over a Joukowski airfoil and the background material needed to understand this problem are discussed in a collection of CDF files available at[1].
Snapshot 1: thick symmetric airfoil at moderate angle of attack
Snapshot 2: thin cambered airfoil at moderate angle of attack
Snapshot 3: thick cambered airfoil at high angle of attack; potential flow gives no information about when separation occurs
References
References
[1] R. L. Fearn. "Two-Dimensional Potential-Flow Aerodynamics." (Feb 2, 2017) plaza.ufl.edu/rlf/Richard L. Fearn.
External Links
External Links
Permanent Citation
Permanent Citation
Richard L. Fearn
"Joukowski Airfoil: Aerodynamic Properties"
http://demonstrations.wolfram.com/JoukowskiAirfoilAerodynamicProperties/
Wolfram Demonstrations Project
Published: February 3, 2017