Gauss Sum Walks

modulus m

971

animate

randomize m

restrictions on m:

composite

prime

prime mod 24:

1 mod 24	5 mod 24
7 mod 24	11 mod 24
13 mod 24	17 mod 24
19 mod 24	23 mod 24

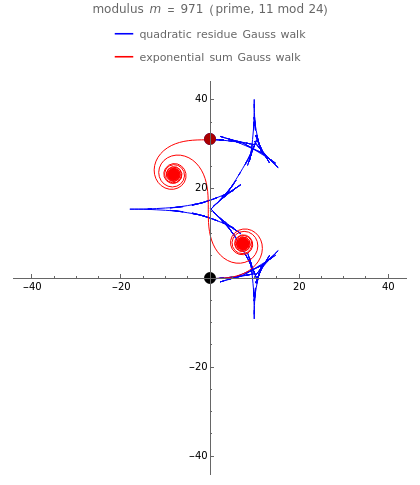
This Demonstration shows two types of pseudorandom walks constructed from Gauss sums, an exponential (red) and a quadratic residue (blue) Gauss walk. The random walk starts at the origin, takes steps given by the terms of the exponential or quadratic residue Gauss sum modulo

, and ends at the value of the Gauss sum. By a famous result of Gauss, if the modulus

is a prime number, the two walks always end at the same point, located at

(0,

)

(

,0)

depending on the remainder of

modulo 4. The exponential Gauss walk has a characteristic shape consisting of two spirals. The quadratic residue Gauss walk exhibits a more complex behavior whose shape is roughly determined by the remainder of

modulo 24.

Details

Given an integer

m>2

, the exponential sum version of the Gauss sum modulo

is defined by

(m)=

∑

n=1

2πi

and the quadratic residue version is defined by

(m)=

m-1

∑

n=1

2πin/m

where

is the Jacobi symbol, which has values 0, 1,

-1

depending on the quadratic residue properties of

modulo

A famous result of Gauss states that when the modulus

is a prime

, the two sums

(p)

and

(p)

have the same value

G(p)

, given by

G(p)=

p	ifp≡1mod4
i p	ifp≡3mod4

For composite moduli

, the two sums are in general different, and the above formula does not necessarily hold.

It was shown by Lehmer[1] that the exponential Gauss walk always has the spiral-type shape observed in the visualization. On the other hand, the shape of the quadratic residue Gauss walk is more mysterious and has not been explored in the literature.

References

[1] D. H. Lehmer, "Incomplete Gauss Sums," Mathematika, 23(2), 1976 pp. 125–135. doi:10.1112/S0025579300008718.

External Links

Successive Differences and Accumulations of the Jacobi Symbol

Gaussian Sum (Wolfram MathWorld)

Legendre Symbol (Wolfram MathWorld)

Jacobi Symbol (Wolfram MathWorld)

Quadratic Residue (Wolfram MathWorld)

Permanent Citation

Erqian Wang

"Gauss Sum Walks"
http://demonstrations.wolfram.com/GaussSumWalks/
Wolfram Demonstrations Project
Published: June 22, 2020