Conway Triangle Notation
Conway Triangle Notation
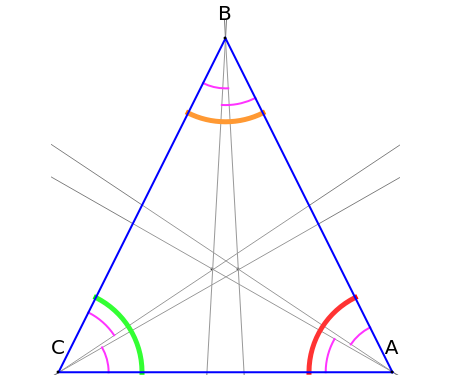
John Horton Conway invented notation that enables more compact formulas for trigonometric functions associated with a triangle.
Let the triangle have sides , , ; internal angles , , ; and Brocard angle .
ABC
a
b
c
∠A
∠B
∠C
ω
Define
S=2Δ=2ABC
S
ϕ
S=++
S
A
S
B
S
B
S
C
S
C
S
A
S
A
2
b
2
c
2
a
2
S
B
2
c
2
a
2
b
2
S
C
2
a
2
b
2
c
2
S
ω
2
a
2
b
2
c
2
S
A
S
B
S
C
External Links
External Links
Permanent Citation
Permanent Citation
Minh Trinh Xuan
"Conway Triangle Notation"
http://demonstrations.wolfram.com/ConwayTriangleNotation/
Wolfram Demonstrations Project
Published: May 11, 2022