Integrals over Dirac Delta Function Representations

R

n

(x)

rectangle

Gaussian

Lorentzian

index

n

1

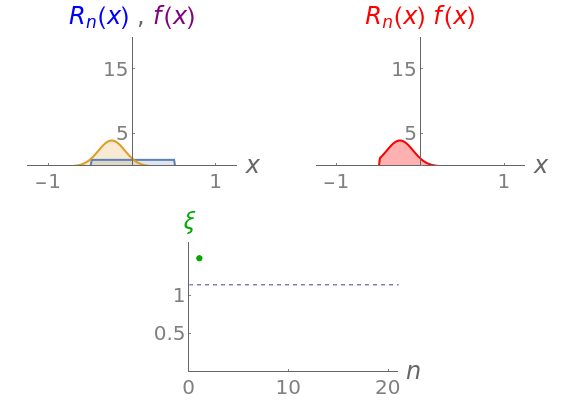
This Demonstration compares the integral of a test function

f(x)=4

-20

2

(x+1/4)

e

multiplying three different representations of the Dirac delta function,

R

n

(x)

, as the index

n

is increased. For each representation,

δ(x)=

lim

n→∞

R

n

(x)

. The three representations are (1) rectangle

R

n

(x)=n,-

1

2n

≤x≤

1

2n

; (2) Gaussian

R

n

(x)=

n

2π

-

2

n

2

x

/2

e

; and (3) Lorentzian

R

n

(x)=

n/π

1+

2

n

2

x

. The top panels show plots of

f(x)

,

R

n

(x)

, and their product. The lower panel shows the integral of the product,

ξ=

∞

∫

-∞

R

n

(x)f(x)dx

, and how it approaches

f(0)=1.15

asymptotically as the index

n

is increased.

External Links

Delta Function (Wolfram MathWorld)

Representations of the Dirac Deltafunction

Permanent Citation

Porscha McRobbie, Eitan Geva

"Integrals over Dirac Delta Function Representations"
http://demonstrations.wolfram.com/IntegralsOverDiracDeltaFunctionRepresentations/
Wolfram Demonstrations Project
Published: March 7, 2011