連想を用いた数値計算プログラミングのアイデア

はじめに
計算速度よりもプログラミングの正確さや改変のしやすさにより重点がある数値計算の場合、Mathematicaを用いたプログラミングに大きなアドバンテージがあります。ここでは、Mathematicaで可能なより効率的かつ間違いの少ないプログラミング方法として、連想を用いた方法を紹介します。
今回のプログラムの内容は四次関数の極値を求める簡単なものですが、より複雑なプログラムにも応用できます。
Global

Definitions, pre-calculations

プログラムで一貫して使われ、変更されない定数や数式などはグローバルに定義しておきます。また、入力する変数によらず計算できるものはここで計算しておくことで実行時間を短縮できます。
注意すべきことは、変数など実行時に変更したいものはグローバルに定義しないことです。変数がグローバルに漏れると予期しないバグの原因になり得ます。
In[]:=
V=1/8*(ϕ^2-1)^2+Δ*(ϕ-1);
In[]:=
V1=D[V,ϕ];
In[]:=
V2=D[V,ϕ,ϕ];
In[]:=
extrema=SolveValues[D[V,ϕ]==0,ϕ];

Physical constants and unit conversion

（このプログラムでは使用しないので）余談ですが、値が十分定まっている物理定数などは手入力しなくても直接欲しい単位で取得できます。数値の打ち間違えや単位変換の間違いを防ぐことができます。誤差が大きい定数や、定義に幾つかの流儀があるものなどは注意が必要です。
In[]:=
me=QuantityMagnitude
electron
PARTICLE

mass
,"Gigaelectronvolts""SpeedOfLight"^2;
In[]:=
mp=QuantityMagnitude
proton
PARTICLE

mass
,"Gigaelectronvolts""SpeedOfLight"^2;
In[]:=
αem=QuantityMagnitude[
α
,1];
例えば自然単位系への変換定数は以下のようになります。
In[]:=
kelvin=QuantityMagnitude[Quantity["Kelvins"],"Gigaelectronvolts"/"BoltzmannConstant"];
In[]:=
gram=QuantityMagnitude[Quantity["Grams"],"Gigaelectronvolts"/"SpeedOfLight"^2];
Main Routines

Find the extrema of the potential

作成したいプログラムを小さな作業のまとまりに分け、それぞれをモジュールとしてコーディングしていきます。
モジュールの入出力は連想を用いて統一し、入力と出力の両方が名前付きで格納されます。これにより、数値の取り出し間違いが減り、デバッグもしやすくなります。
​
ここでは、ポテンシャルVの極値を求める最初のモジュールで
<|”Δ”0.1|>
を入力とし、
Δ0.1,vTV-1.08803,vFV0.878885,vTop0.209149
を出力するものを作成します。
In[]:=
getExtremaA[input_]:=​​Block[(*BlockもしくはModule*)​​(*ここで計算に必要になる値を取り出しておきます。また、グローバルにローカル変数が漏れないように注意します。*)​​{Δ=input["Δ"],sorted},​​sorted=SortBy[Re[extrema],V/.ϕ->#&];​​(*出力は入力に加える形で行います*)​​<|input,"vTV"->sorted[[1]],"vFV"->sorted[[2]],"vTop"->sorted[[3]]|>]
異なるアルゴリズムを比較したい場合、出力が同じになるようにモジュールを作成することで、いつでもアルゴリズムを変更してプログラムを実行できます。
In[]:=
getExtremaB[input_]:=Block[{Δ=input["Δ"],sorted},​​sorted=SortBy[NSolveValues[V1==0,ϕ],V/.ϕ->#&];​​<|input,"vTV"->sorted[[1]],"vFV"->sorted[[2]],"vTop"->sorted[[3]]|>]

Mass at the false vacuum

次に、二つ目のモジュールを作成しましょう。
​
ここでは、ポテンシャルの2階微分の値を極値の一つで求めるモジュールを作成します。
In[]:=
getMassFV[input_]:=Block[{Δ=input["Δ"],ϕ=input["vFV"]},​​<|input,"mFV"->Sqrt[V2]|>]
前のモジュールの出力が次のモジュールの入力となり、すべての途中結果が保存されます。これによって、何かおかしな結果が出たときに遡ってデバッグが可能になります。
​
また、モジュール作成時には前のモジュールまでの計算を一時的に保存し、テスト入力として使用することでデバッグ時間を短縮できます。
In[]:=
tempResult=getExtremaA@<|"Δ"0.1|>;
In[]:=
tempResult2=getExtremaA@<|"Δ"0.2|>;
In[]:=
"mFV"/.getMassFV/@{tempResult,tempResult2}
Out[]=
{0.811578,0.0659034}
Results
作成したモジュールは/@や@などを用いて合成し、全体のプログラムを構築します。
In[]:=
myProgram=getMassFV@getExtremaA@#&;
In[]:=
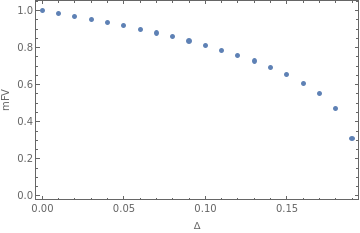
resultA=myProgram/@Table[<|"Δ"->Δ|>,{Δ,0.,0.19,0.01}];
In[]:=
ListPlot[{"Δ","mFV"}/.resultA,Frame->True,FrameLabel->{"Δ","mFV"}]
Out[]=
もし結果がおかしかった場合、途中結果を使ってデバッグすることも可能です。
In[]:=
ListPlot[{"vFV","mFV"}/.resultA,Frame->True,FrameLabel->{"vFV","mFV"}]
Out[]=
異なるアルゴリズムで計算し、結果を比較することも簡単にできます。
In[]:=
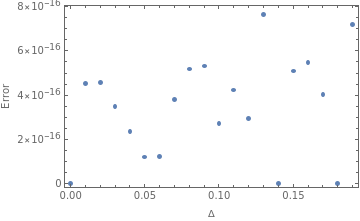
resultB=getMassFV/@getExtremaB/@Table[<|"Δ"->Δ|>,{Δ,0.,0.19,0.01}];
In[]:=
ListPlot[{"Δ"/.resultA,(("mFV"/.resultA)-("mFV"/.resultB))/("mFV"/.resultA)},Frame->True,FrameLabel->{"Δ","Error"}]
Out[]=
おわりに
ここでは簡単な例を用いて連想を用いたプログラミングについて紹介しました。特に結果の正確さや計算方法の比較などに重点がある数値計算を行う場合、今回紹介した方法が参考になればと思います。また、速度が重要な数値計算においても、最初にMathematicaで簡単なプロトタイプを作っておくことにより、RustやC言語などで書いたプログラムのデバッグとして役に立ちます。