A Model for Fermi-Dirac Integrals
A Model for Fermi-Dirac Integrals
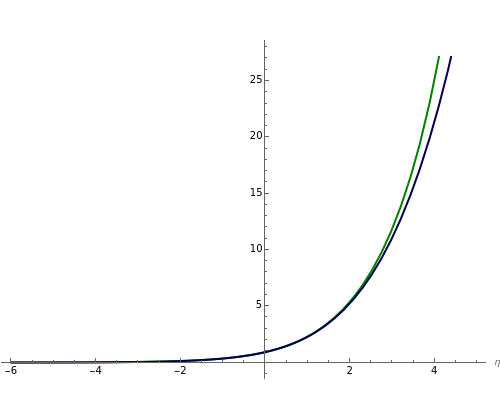
Fermi–Dirac integrals arise in calculating pressure and density in degenerate matter, such as neutron stars; they also occur in the electronic density of semiconductors. A (semi-)closed form was not known until 1995, when Howard Lee noticed the application of the integral form of polylogarithms. We developed an alternative expression, (η)=dx (plotted here), using an exponential model that is accurate for (arXiv:0909.3653v5 [math.GM]). Here we compare the model, in green, with the polylogarithm expression, in blue, for Fermi–Dirac integrals half-integer order , with (orders commonly used in astrophysics and semiconductors).
F
k/2
1
Γ1+
k
2
∞
∫
0
k/2
x
1+
x-η
e
η<3
k
2
k=-1,1,3,5
Details
Details
Briefly, the model is based on the idea of rewriting as a product of and a function that is a basic exponential model; for more details, see[1]. The dependence on the factor explains the restriction to values .
k/2
x
1+
x-η
e
k/2
x
1+
x
e
η
e
η<3
Written in terms of polylogarithms, the (normalized) Fermi–Dirac integral is[2] (η)=-(-).Meanwhile, the model is found to be (η)=(1-)ζ1+--1+1ζ1+,-ζ1+,c(k,η)+1,where is a function written in terms of the Lambert function (see[1] and references therein).
F
k/2
Li
1+k/2
η
e
F
k/2
η
e
-k/2
2
k
2
η
e
-η
e
-k/2
2
k
2
c(k,η)+1
2
k
2
c(k,η)
References
References
[1] M. H. Lee, "Polylogarithmic Analysis of Chemical Potential and Fluctuations in a d-Dimensional Free Fermi Gas at Low Temperatures," Journal of Mathematical Physics, 36, 1995 pp. 1217–1231.
External Links
External Links
Permanent Citation
Permanent Citation
Michael Morales
"A Model for Fermi-Dirac Integrals"
http://demonstrations.wolfram.com/AModelForFermiDiracIntegrals/
Wolfram Demonstrations Project
Published: April 6, 2012