Euler-Maclaurin Summation Formula
Euler-Maclaurin Summation Formula
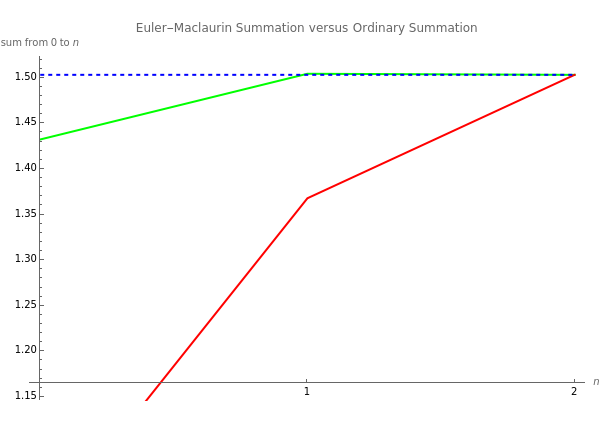
The Euler–Maclaurin summation formula transforms a sum over the values of a function to a sum over the derivatives of a function. Its main advantage is that the new sum usually converges much more quickly than original. One must be careful, though, as the error term may not go to zero as more and more terms in the series are taken, as is shown by .
ln(1+k)
The blue line represents the value of the sum to terms in the series. The red line represents the progression of the sum after terms. The green line represents the progression of the Euler–Maclaurin sum after terms.
n
n
n
Details
Details
The Euler–Maclaurin formula reads f(k)=f(k)dk++((N)-(0))+,where is the Bernoulli number and is a remainder term. The power of the Euler–Maclaurin summation formula lies in how quickly the new sum converges, even if the error term is unbounded.
N
∑
k=0
N
∫
0
f(N)+f(0)
2
m
∑
k=1
B
2k
(2k)!
(2k-1)
f
(2k-1)
f
R
m
B
n
th
n
R
m
External Links
External Links
Permanent Citation
Permanent Citation
Sam Nicoll
"Euler-Maclaurin Summation Formula"
http://demonstrations.wolfram.com/EulerMaclaurinSummationFormula/
Wolfram Demonstrations Project
Published: January 23, 2012