Pólya's Urn

display

sample

initial settings

black

3

white

3

increase sample by 20

sample size = 20

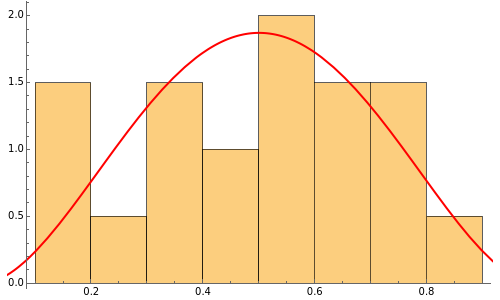
Initially, an urn contains

b

black marbles and

w

white ones. Every minute, one marble is chosen from the urn at random and replaced, together with another marble of the same color. The proportion of black marbles in the urn after

n

minutes is the random variable

B

n

. The sequence of random variables is a martingale, and thus converges almost surely to a limit random variable

Z

. This limit random variable

Z

has the beta distribution

β(b,w)

. This Demonstration enables you either to plot the graph of

B

n

against

n

for 1000 minutes, demonstrating the convergence, or to take samples of the random variable

B

1000

, comparing histograms of the resulting data with the PDF of the beta distribution.

Details

G. R. Grimmett and D. R. Stirzaker, Probability and Random Processes, Oxford: Oxford University Press, 1982.

"Urn problem," Wikipedia.

External Links

Martingale (Wolfram MathWorld)

Permanent Citation

Mark Hennings

"Pólya's Urn"
http://demonstrations.wolfram.com/PolyasUrn/
Wolfram Demonstrations Project
Published: March 7, 2011