Bound-State Spectra for Two Delta Function Potentials

strength of the δ function potential λ

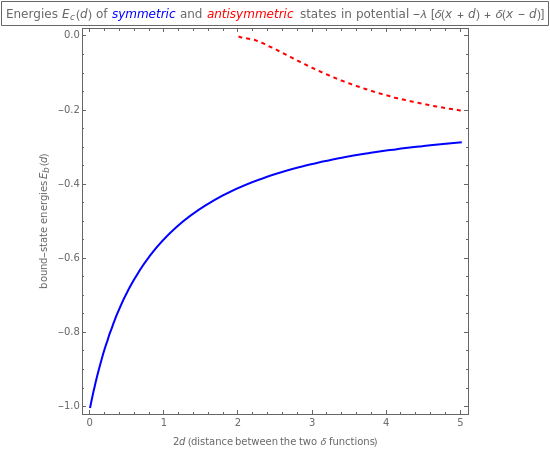
This Demonstration shows the bound-state spectra

(d)

of a particle of mass

in the presence of two attractive

potentials separated by a distance

V(x)=-λ[δ(x+d)+δ(x-d)]

. Since the Fourier transform of this potential is factorizable,

V(k-k')=-2λcos((k-k')a)=-2λ[cos(ka)cos(k'a)+sin(ka)sin(k'a)]

, the bound-state spectra are easily obtained using the momentum-space Schrödinger equation. The energies are normalized to the magnitude of the symmetric-state energy at

d=0

. Note that the second (antisymmetric) bound state appears only when the distance between the

functions exceeds the critical value

ℏ

/λm

Details

Snapshot 1: typical symmetric and antisymmetric bound-state energies

(d)

as a function of distance

between the two attractive

functions

Snapshot 2: for a weak potential strength

λ<<1

, a second bound-state, the antisymmetric state, appears only when the distance between the two

functions is large,

2d>>1

Snapshot 3: for a strong potential

λ>>1

, the symmetric and antisymmetric states become degenerate when the distance

between the two

functions is increased

Analytical and numerical treatment of the Schrodinger equation in momentum space can be found in W. A. Karr, C. R. Jamell, and Y. N. Joglekar, "Numerical Approach to Schrodinger Equation in Momentum Space," arXiv, 2009.

External Links

Delta Function (Wolfram MathWorld)

Schrödinger Equation (ScienceWorld)

Permanent Citation

Christopher R. Jamell, Yogesh N. Joglekar

"Bound-State Spectra for Two Delta Function Potentials"
http://demonstrations.wolfram.com/BoundStateSpectraForTwoDeltaFunctionPotentials/
Wolfram Demonstrations Project
Published: March 7, 2011