Primitive Pythagorean Triples 2: Ordered Pairs
Primitive Pythagorean Triples 2: Ordered Pairs
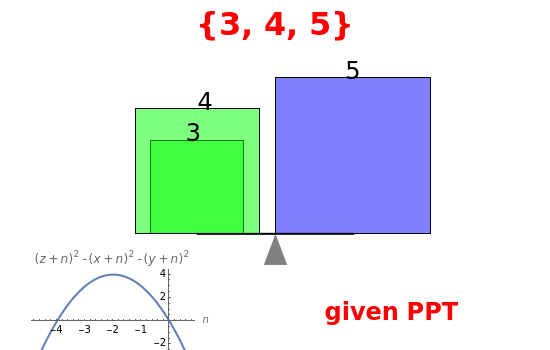
Multiplying all three sides of a right triangle by the same number yields another right triangle because of similarity. This Demonstration illustrates that it is always possible to find a number to add to all three elements of any Pythagorean triple to generate another Pythagorean triple.
n
Details
Details
Let be a Pythagorean triple (PT), that is, , , and are positive integers such that +=. A primitive Pythagorean triple (PPT) is a PT with .
{x,y,z}
x
y
z
2
x
2
y
2
z
gcd(x,y,z)=1
If negative values for are allowed, then a second PT can be obtained by adding a single unique integer value to each of the three original PT elements: . Redundant forms of PTs are obtained by allowing negative values. The unique value of that works is .
{x,y,z}
n
{x+n,y+n,z+n}
n
n=-2(x+y-z)
The triangle represented by the derived PT has the following properties.
T'
T'
T'
T'
This pairing of PPTs provides a way to number them.
Notice that names have been given to the results. The identification of parent and the numbering of children is used to make the set of all PPTs a well-ordered set. This ordering was used to implement the "given PPT" slider (with values shown in base 3).
The simple quadratic form of the graph displayed shows that exists and is unique.
n
Assume that
2
(z+n)
2
(x+n)
2
(y+n)
2
z
2
x
2
y
n≠0
Then
2
(z+n)
2
(x+n)
2
(y+n)
2
z
2
x
2
y
Expand and cancel to get
-n(n+2x+2y-2z)=0
so that the unique solution is
n=-2(x+y-z)
External Links
External Links
Permanent Citation
Permanent Citation
Robert L. Brown
"Primitive Pythagorean Triples 2: Ordered Pairs"
http://demonstrations.wolfram.com/PrimitivePythagoreanTriples2OrderedPairs/
Wolfram Demonstrations Project
Published: April 11, 2011