Gram-Schmidt Process in Two Dimensions
Gram-Schmidt Process in Two Dimensions
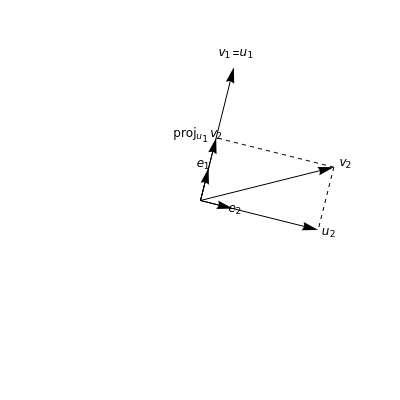
The Gram-Schmidt process is a means for converting a set of linearly independent vectors into a set of orthonormal vectors. If the set of vectors spans the ambient vector space, then this produces an orthonormal basis for the vector space.The Gram-Schmidt process is a recursive procedure. After the first vectors have been converted into orthonormal vectors, the difference between the original vector and its projection onto the space spanned by the first orthonormal vectors is normalized to obtain the vector in the orthonormal collection.In two dimensions, start with a vector = and normalize it to obtain =. Next, project onto and compute , the difference between and this projection. Finally, normalize this vector to obtain .
k-1
k-1
th
k
k-1
th
k
v
1
u
1
e
1
v
1
||||
v
1
v
2
v
1
u
2
v
2
e
2