Convexity and Intersection in Polygons
Convexity and Intersection in Polygons
Introduction
Introduction
Polygons may be characterized by their convexity or type of non-convexity:
Convex Polygons
Convex Polygons
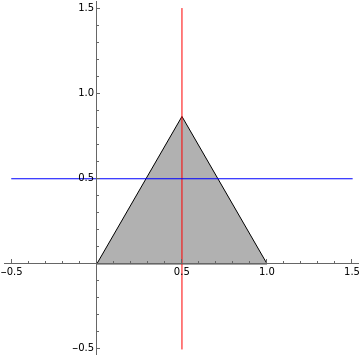
A convex polygon is one where any line drawn through the polygon (and not tangent to an edge or corner) meets its boundary exactly twice. As a consequence, all its interior angles are less than 180°. Equivalently, any line segment with endpoints on the boundary passes through only interior points between its endpoints. This condition is true for polygons in any geometry, not just Euclidean.
Non-Convex Polygons
Non-Convex Polygons
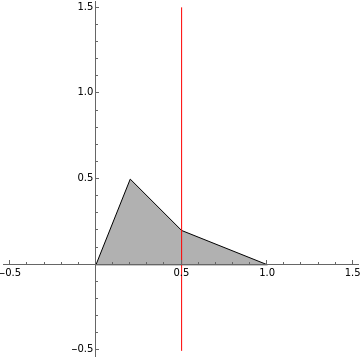
A non-convex polygon is one where a line may be found which meets its boundary more than twice. Equivalently, there exists a line segment between two boundary points that passes outside the polygon.
Simple Polygons
Simple Polygons
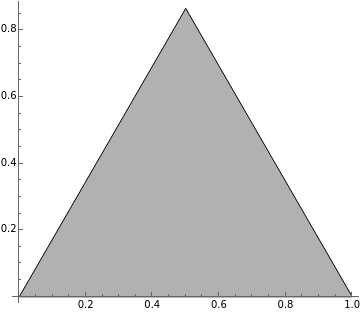
A simple polygon is one where the boundary of the polygon does not cross itself. All convex polygons are simple.
Concave Polygons
Concave Polygons
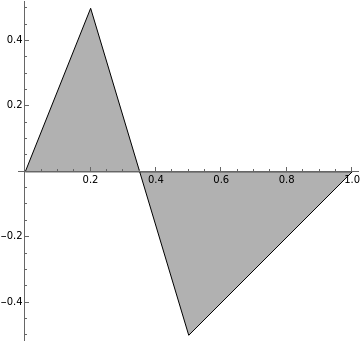
A concave polygon is non-convex and simple. There is at least one interior angle greater than 180°.
Star-Shaped Polygons
Star-Shaped Polygons
A star-shaped polygon is one where the whole interior is visible from at least one point, without crossing any edge. The polygon must be simple, and may be convex or concave. All convex polygons are star-shaped.