You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
In[]:=
settings=<|"ωc"2Pi*100,"ϵ"0.3|>
Out[]=
ωc200π,ϵ0.3
First kind Chebyshev filter transfer function
First kind Chebyshev filter transfer function
Low pass
Low pass
In[]:=
pole[ωc_,ϵ_,n_,k_]:=-ωc*Sinh[ArcSinh[1/ϵ]/n]Sin[(2k+1)/(2n)*Pi]+I*ωc*Cosh[ArcSinh[1/ϵ]/n]Cos[(2k+1)/(2n)*Pi]
In[]:=
H[n_,s_]:=Block[{ωc=settings[["ωc"]],ϵ=settings[["ϵ"]]},Product[-pole[ωc,ϵ,n,k],{k,0,n-1}]/Product[s-pole[ωc,ϵ,n,k],{k,0,n-1}]/If[EvenQ[n],Sqrt[1+ϵ^2],1]]
In[]:=
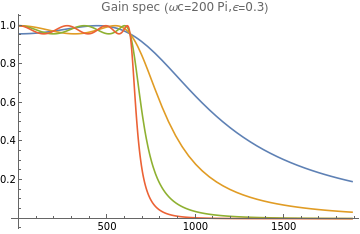
Plot[{Abs[H[2,I*ω]],Abs[H[3,I*ω]],Abs[H[5,I*ω]],Abs[H[7,I*ω]]},{ω,0,3*settings[["ωc"]]},PlotRangeFull,PlotLegends{"n=2","n=3","n=5","n=7"},PlotLabel"Gain spec (ωc="<>ToString[settings[["ωc"]]]<>",ϵ="<>ToString[settings[["ϵ"]]]<>")"]
Out[]=
In[]:=
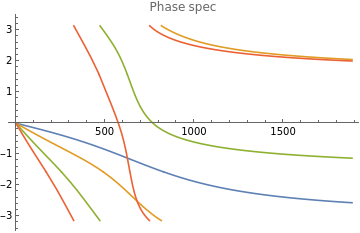
Plot[{Arg[H[2,I*ω]],Arg[H[3,I*ω]],Arg[H[5,I*ω]],Arg[H[7,I*ω]]},{ω,0,3*settings[["ωc"]]},PlotRangeFull,PlotLegends{"n=2","n=3","n=5","n=7"},PlotLabel"Phase spec"]
Out[]=
High pass
High pass
H2[n_,s_]:=Block[{ωc=settings[["ωc"]],ϵ=settings[["ϵ"]]},Product[pole[ωc,ϵ,n,k],{k,0,n-1}]/Product[-ωc^2/s+pole[ωc,ϵ,n,k],{k,0,n-1}]/If[EvenQ[n],Sqrt[1+ϵ^2],1]]
In[]:=
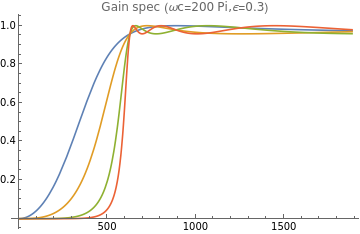
Plot[{Abs[H2[2,I*ω]],Abs[H2[3,I*ω]],Abs[H2[5,I*ω]],Abs[H2[7,I*ω]]},{ω,0,3*settings[["ωc"]]},PlotRangeFull,PlotLegends{"n=2","n=3","n=5","n=7"},PlotLabel"Gain spec (ωc="<>ToString[settings[["ωc"]]]<>",ϵ="<>ToString[settings[["ϵ"]]]<>")"]
Out[]=
In[]:=
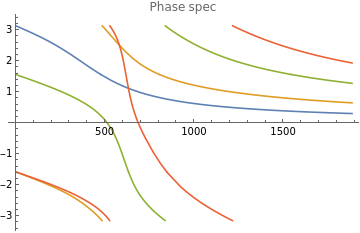
Plot[{Arg[H2[2,I*ω]],Arg[H2[3,I*ω]],Arg[H2[5,I*ω]],Arg[H2[7,I*ω]]},{ω,0,3*settings[["ωc"]]},PlotRangeFull,PlotLegends{"n=2","n=3","n=5","n=7"},PlotLabel"Phase spec"]
Out[]=