Instructions for running this notebook
Instructions for running this notebook
Environment variables
Environment variables
Data sources
Data sources
Utilities
Utilities
Dimensionality of Politics
Dimensionality of Politics
Politics is often described by placing things on a left-right spectrum. For example, one Senator might be described as "to the left" of another, or a bill as "right-leaning" etc. This doesn't capture all the nuances of politics, but it roughly approximates the overall large-scale structure.
This process is essentially equivalent to dimension reducing all of politics down to a single dimension. It works because even though politics is, in principle, very high-dimensional, in practice most of the variance can be described with a single dimension.
"One-dimensional politics" cannot represent the nuance of inherently high-dimensional issues, so the dimensionality of politics can help measure the ability of politics to represent nuance.
Using roll-call voting data from the US Congress, US Supreme Court, and the German Bundestag, it is possible to quantify the extent to which politics can be reduced to a single dimension, and more generally, how high-dimensional voting behavior is.
Vote Matrices
Vote Matrices
The vote matrix for a particular voting body (e.g. the US Senate) is a matrix with a row for every member (e.g. Senator) and a column for every issue voted on (e.g. Bill). There is a 1 in every position of the matrix if the corresponding member voted affirmatively for the corresponding bill, a -1 if they voted negatively, and a 0 otherwise (e.g. they abstained).
In[]:=
MatrixPlot[senateVoteMatrices[{117,"Senate"}]["VoteMatrix"],FrameLabel{"Senator","Bill"},PlotRangePadding->0,FrameTicks->None]
Out[]=
(Matrix plot of the transpose of the vote matrix for the Senate of the 117th Congress. Orange represents 1, blue -1, and white 0.)
Each row of this vote matrix gives the legislative record of a particular Senator, and each column gives the record of which Senators voted for a particular bill.
Dimension Reduction
Dimension Reduction
Principal component analysis (PCA) is a standard dimension reduction technique that can be used to "compress" high-dimensional data into fewer dimensions (principal components). The principal components are conventionally sorted by the amount of the variance they explain. For example, plot below shows the results of using PCA to reduce each of the Senators of the 117th Congress down to the two dimensions that explain the most variance:
In[]:=
drPlot2D[data_,opts___]:=With[{parties=Keys@ReverseSort@Counts@data["MemberParties"]},ListPlot[MapThread[Callout[Style[#1,#2],#3,LabelStyle->Tiny]&,{DimensionReduce[data["VoteMatrix"],2,Method->"PrincipalComponentsAnalysis"],partyColor/@data["MemberParties"],data["MemberNames"]}],opts,AspectRatio->Automatic,Frame->True,Axes->None,FrameLabel->{"principal component 1","principal component 2"},PlotLegends->SwatchLegend[partyColor/@parties,Replace[parties,_Missing->"Missing",{1}]]]]
In[]:=
drPlot2D[senateVoteMatrices[{117,"Senate"}],PlotLegends->None]
Out[]=
(Principal components of the vote matrix for the Senate of the 117th Congress.)
As might be expected, political parties form well-defined clusters, with the first principal component approximately corresponding to left-right partisanship. In other congresses, partisanship was less pronounced. For example, this is the same plot for the Senate of the 90th Congress:
In[]:=
drPlot2D[senateVoteMatrices[{90,"Senate"}],PlotLegends->None]
Out[]=
(Principal components of the vote matrix for the Senate of the 90th Congress.)
In the 90th Congress, which started in 1967, the political parties had such similar voting behavior that they can barely be separated by the first two principal components.
One of the useful properties of PCA is that it can give the fraction of the variance described by each reduced dimension. This is often represented in a scree plot which shows the fraction of the variance described by each of the principal components:
In[]:=
scree[mat_]:=Enclose[Module[{filteredMat,standardizedMat,cov},filteredMat=Transpose@Select[Transpose@mat,Variance[#]>0&];ConfirmAssert[Length[filteredMat]=!=0];standardizedMat=Transpose[Standardize[filteredMat]];ConfirmAssert[Length[standardizedMat]>1];cov=Covariance[standardizedMat];Eigenvalues[cov]/ConfirmBy[Tr[cov],#!=0&]],{}&]
In[]:=
ListLinePlot[{scree[N@senateVoteMatrices[{117,"Senate"}]["VoteMatrix"]],scree[N@senateVoteMatrices[{90,"Senate"}]["VoteMatrix"]]},PlotRange->{{1,10},All},Mesh->All,Frame->True,FrameLabel->{"principal component #","fraction of variance"},PlotLegends->{"117th Congress","90th Congress"}]
(Scree plot of the vote matrices of the Senates of the 117th and 90th Congresses.)
This scree plot shows how the first dimension dominates all others in the 117th Congress, while in the 90th Congress the first dimension was important, but not much more important than other dimensions.
Measuring "One-Dimensionality"
Measuring "One-Dimensionality"
By measuring the variance explained by the first principal component, it is possible to measure how much voting behavior can be explained with a single dimension.
This plot shows the fraction of the variance explained by the first principal component over time in both chambers of the US Congress:
In[]:=
DateListPlot[{{#Date,scree[N@#VoteMatrix][[1]]}&/@Values@houseVoteMatrices,{#Date,scree[N@#VoteMatrix][[1]]}&/@Values@senateVoteMatrices},PlotRange->All,InterpolationOrder->0,PlotLegends->{"House","Senate"},FrameLabel->{"time","fraction of variance explained by one dimension"}]
(Fraction of variance described by a single dimension over time in the US House and US Senate.)
This shows that around 20% to 30% of voting behavior could historically be described with a single dimension. However, over the last 60 years or so, that amount has steadily risen to about 60%. This broadly aligns with the a previous project where I looked at measuring the strength of partisanship in voting behavior.
Characterizing Dimensionality
Characterizing Dimensionality
The section above shows how one-dimensional politics is, but that is slightly different from measuring how high dimensional it is. In this section, more general measures of dimensionality are considered. These are inherently fuzzier than the measure of one-dimensionality, but they still provide some insight into the dimensionality of politics.
To illustrate, below are three hypothetical scree plots. In the blue scree plot, most of the variance is described by a single dimension with a long tail of less important dimensions. In the orange scree plot, there are four dimensions that each explain a quarter of the variance, and there is no tail. Finally, in the green plot, there is a sequence of dimensions each explaining less and less variance, but with no clear cutoff:
(Hypothetical scree plots.)
Because four dimensions explain most of the variance, there is a sense in which the orange line represents the scree plot of an approximately four-dimensional dataset. Similarly, the blue line represents the scree plot of an approximately one-dimensional dataset. It is not clear that the dataset producing the green scree plot can be meaningfully assigned an integer number of dimensions, but by analogy to the other scree plots, it should be more than one-dimensional.
(Hypothetical maximal- and one-dimensional cumulative scree plots.)
Therefore, by measuring the area under the cumulative scree plot, we can approximate the dimensionality of the underlying data.
This measure has the beautiful feature that it is essentially the Gini coefficient of the scree plot. The Gini coefficient is traditionally used as a measure of inequality, so it makes sense that it would show up here as low-dimensional data will have a very unequal scree plot.
The only complication is that the number of principal components varies significantly for different datasets, but the number of principal components that matter remains relatively fixed. This means that the proportion of principal components that explain significant variance (which is what the Gini coefficient essentially measures) varies just by the shape of the data. This can be fixed, however, by trimming the scree plots and only looking at the first 50 or so principal components. See the appendix below that shows that the results are not too sensitive to the choice of cutoff.
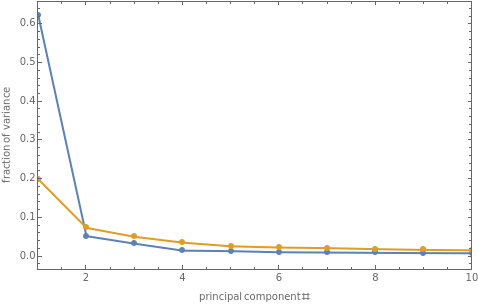
Its also worth noting that patterns like those in the hypothetical scree plots this also appear in real data. For example, the scree plot below compares the Senate of the 56th Congress with a recent block of Supreme Court cases. The first principal components explains about 40% of the variance in both cases, but the later principal components make it clear that voting behavior in the Supreme Court was higher-dimensional:
(Scree plots of vote matrices from the Senate of the 56th Congress (1899) and the Supreme Court (from March 2016 to April 2017).)
(See this note on a previous project about why the absolute values in inter-body comparisons should be taken with a grain of salt.)
Gini Dimensionality Results
Gini Dimensionality Results
The plot below shows dimensionality over time in the US House and Senate (measured as the Gini coefficient of the first 50 points on the scree plot):
(Gini dimensionality in Congress as a function of time. Higher Gini dimensionality corresponds with lower dimensional voting behavior.)
The House and the Senate both follow similar trajectories. Like the plot of one-dimensionality, both the House and the Senate are relatively flat for much of history, hovering around a Gini coefficient of 0.6. However, over the last 60 years it has gradually increased to about 0.8.
Discussion
Discussion
In a previous post, I argued against the use of spatial models to compare the ideological behavior of voting bodies over time. My main objection was that ideology space changes over time, making comparisons of the distributions of points from different times meaningless.
This project is thus a natural extension in that it seeks to measure not the distribution of points in ideology space, but the structure of the underlying ideology space itself. The fact that there are changes to that space over time is further evidence of the dangers of comparing ideal points from different periods in history.
Appendices
Appendices
Robustness to Choice of Gini Cutoff
Robustness to Choice of Gini Cutoff
(Gini dimensionality in the House of Representatives over time with different choices of Gini cutoff.)
Transposed Vote Matrix
Transposed Vote Matrix
In this post, the dimensionality of politics was measured by the number of dimensions required to which bills a given voting member (e.g. Senator) voted for. However, the same analysis can be done with the number of dimensions required to explain which voting members voted for a given bill. This is mathematically equivalent but uses the transpose of the vote matrix.
Here is the one-dimensionality over the House and Senate over time using the transposed vote matrix:
(One-dimensionality of both chambers of Congress over time using the transposed vote matrix.)
The general shape is quite similar to what was produced before using the normal vote matrix.
Here is the Gini dimensionality plot using the transposed vote matrix:
(Gini dimensionality of both chambers of Congress over time using the transposed vote matrix.)
Again, the general trend is similar to that which was generated using the normal vote matrix.
Extending to Other Voting Bodies
Extending to Other Voting Bodies
All of the methods presented here can be applied to any voting body for which we can generate vote matrices. It is surprisingly hard to get roll call voting data, especially for voting bodies outside the US. However, as discussed in a previous project that also involved roll call voting data, it is possible to get good data for the US Supreme Court (through the Washington University Law Supreme Court Database) and the German Bundestag (through BTVote).
I should also note again that comparisons between absolute values between different voting bodies should be taken with a grain of salt. See this note on a previous project for more explanation.
Bundestag
Bundestag
(One-dimensionality of the Bundestag over time.)
And this shows the Gini dimensionality:
(Gini dimensionality of the Bundestag over time.)
Supreme Court
Supreme Court
Unlike Congress and the Bundestag where the composition of the voting body changes at regular intervals (at elections), the Supreme Court changes gradually and irregularly as justices leave the court and new justices are appointed. The intervals between personnel changes (sometimes call natural courts) will be used for the analysis here.
This plot shows the one-dimensionality of the Supreme Court over time:
(One-dimensionality of the Supreme Court over time.)
And this shows the Gini dimensionality with a Gini cutoff of 10 because of the smaller size of the Court:
(Gini dimensionality of the Supreme Court over time.)
Both plots show high variance, but this is likely a consequence of small sample sizes especially for short natural courts.
Dimension Reduction Plots
Dimension Reduction Plots
In the beginning of this post, I showed some plots of dimension-reduced vote matrices from the US Senate. This linked PDF contains similar plots for every meeting for which I have data for the US House, US Senate, US Supreme Court, and German Bundestag.
Notes
Notes