Japanese Theorem for Three Tangent Circles and a Triangle
Japanese Theorem for Three Tangent Circles and a Triangle
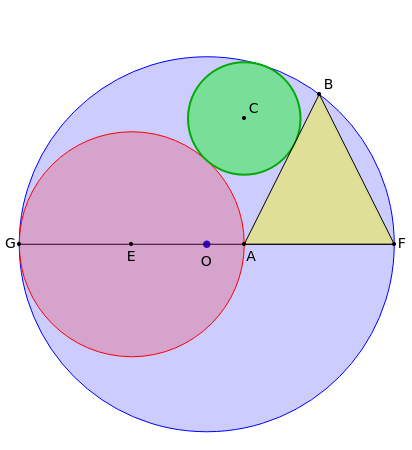
This Japanese classical theorem (Sangaku) deals with a configuration of three tangent circles (blue, purple and green) and an isosceles triangle that is tangent to one of the three circles (green) and has two of its vertices on the circumference of the largest circle (blue). The theorem states that the line joining the left vertex of the triangle to the center of the green circle is perpendicular to the horizontal diameter.
Details
Details
Each of the three circles is tangent to the other two. The green circle is tangent to the side of the yellow isosceles triangle. The theorem states that the line from to is perpendicular to the diameter of the blue circle. You can change the position of the center of the purple circle.
AB
A
C
GF
Click the "configuration" button to see the triangle and circles. Click the "line AC" button to see the subject of the theorem. Click the "auxiliary points and lines" button to see the construction used in the proof of the theorem.
External Links
External Links
Permanent Citation
Permanent Citation
Tomas Garza
"Japanese Theorem for Three Tangent Circles and a Triangle"
http://demonstrations.wolfram.com/JapaneseTheoremForThreeTangentCirclesAndATriangle/
Wolfram Demonstrations Project
Published: August 4, 2022