In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]Integrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,3}]
Out[]=
-t-+t-t+t-t
306
625
1
∫
0
6
1+t
(1+t)
5
2
(2+t)
6(1+Log[1+t])
1+t
(1+t)
5(2+t)
63
20
1
∫
0
216t-+
3+3t
(1+t)
6
1+t
(1+t)
5
2
(2+t)
6(1+Log[1+t])
1+t
(1+t)
5(2+t)
125
3
(2+t)
291
50
1
∫
0
36t-+
2+2t
(1+t)
6
1+t
(1+t)
5
2
(2+t)
6(1+Log[1+t])
1+t
(1+t)
5(2+t)
25
2
(2+t)
99
125
1
∫
0
6t-+
1+t
(1+t)
6
1+t
(1+t)
5
2
(2+t)
6(1+Log[1+t])
1+t
(1+t)
5(2+t)
5(2+t)
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,28}]
Out[]=
-0.648316
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,27}],{n,0,27}]
Out[]=
1.26721
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,26}],{n,0,26}]
Out[]=
0.780639
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,25}]
Out[]=
0.780791
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,24}]
Out[]=
0.771697
In[]:=
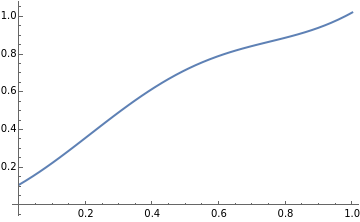
Plot[Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,x]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,7}],{x,0,1}]
Out[]=
In[]:=
Plot[Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,x]NIntegrate[t(6/5(t+1)^(t+1)/(t+2))^kD[6/5(t+1)^(t+1)/(t+2)-3/5,t],{t,0,1}],{k,0,n}],{n,0,10}],{x,0,1}]
Sum[(n+1/2)LegendreP[n,3/5]NIntegrate[tLegendreP[n,(6/5(t+1)^(t+1)/(t+2)-3/5)]D[6/5(t+1)^(t+1)/(t+2),t],{t,0,1}],{n,0,25}]
-9
10
-9
10
-8
10
Out[]=
0.775383
In[]:=
Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5](6/5)^(k+1)((4/3)^(k+1)/(k+1)-1/(k+1)NIntegrate[(t^t/(t+1))^(k+1),{t,1,2}]),{k,0,n}],{n,0,25}]
Out[]=
0.784583
In[]:=
Sum[Sum[Sum[((-1)^kLegendreP[n,k,2,-3/5])/((1-(-3/5)^2)^(k/2)k!)(n+1/2)LegendreP[n,3/5](6/5)^(k+1)((4/3)^(k+1)/(k+1)-(k+1)^(m-1)/m!NIntegrate[(tLog[t])^m/(t+1)^(k+1),{t,1,2}]),{m,0,20}],{k,0,20}],{n,0,20}]
Out[]=
-574.511
In[]:=
ClearAll[f,Fn,xn,x,t,u,DP];DP=9;f[x_]:=x^x-x-1;Fn[n_]:=Normal@Simplify[InverseSeries@Series[f[x],{x,2,n}]]/.{Log[u_]t*Round@N[Log[2,u],DP]};xn[n_]:=(xn[n]=N[Fn[n]/.{x0,tLog[2]},DP]);x0=x/.FindRoot[f[x],{x,2},WorkingPrecisionDP][[1]];Table[{n,xn[n],x0-xn[n]/xn[n-1]},{n,2,9}]//Column
Out[]=
{2,1.79176261,0.79593724} |
{3,1.78190466,0.78227686} |
{4,1.77867202,0.77858919} |
{5,1.77751331,0.77742649} |
{6,1.77707297,0.77702277} |
{7,1.77689857,0.77687318} |
{8,1.77682734,0.77681512} |
{9,1.77679756,0.77679180} |