24a. Construct a Triangle Given the Length of the Altitude to the Base, the Difference of Base Angles and the Sum of the Lengths of the Other Sides

δ

0.8

s

1.4

length of altitude from C to AB

h

C

0.5

move A'

0.5

show solution

This Demonstration shows a marked-ruler (or verging) construction of a triangle

ABC

given the length

h

C

of the altitude to the base, the difference

δ

of angles at the base and the sum

s

of the lengths of the other two sides.

Construction

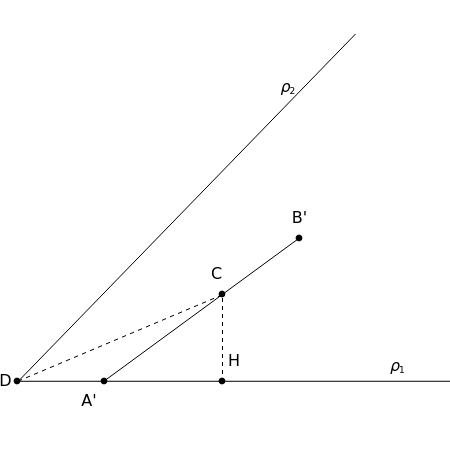
From a point

D

draw two rays

ρ

1

and

ρ

2

at an angle

δ

.

Let

H

be on

ρ

1

such that

HD=h

. Let

C

be the intersection of the angle bisector of the angle

ρ

1

ρ

2

and the perpendicular to

ρ

1

at

H

. Thus

∠CDH=δ/2

and

DHC

is a right triangle with hypotenuse

DC

.

Draw the line segment

A'B'

of length

s

with

C

between

A'

and

B'

and

A'

on

ρ

1

.

Move

A'

along

ρ

1

until

B'

is on

ρ

2

; call this point

F

. Then set

A=A'

.

Let

B

be the reflection of

A

in

DC

.

Then

ABC

satisfies the stated conditions.

Proof

In the triangle

DAF

,

∠FDA=δ

,

∠AFD=β

, but the exterior angle

∠FAB=α

, so

δ=α-β

.

Triangles

DCF

and

DCB

are congruent, so

CB=CF

, and

BC+CA=a+b

.

Details

This is a verging, or marked-ruler construction. For verging, see [1, p. 124].

References

[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998.

External Links

Constructing a Square with Sticks of Equal Length

Permanent Citation

Izidor Hafner

"24a. Construct a Triangle Given the Length of the Altitude to the Base, the Difference of Base Angles and the Sum of the Lengths of the Other Sides" from the Wolfram Demonstrations Project http://demonstrations.wolfram.com/24aConstructATriangleGivenTheLengthOfTheAltitudeToTheBaseThe/
Published: October 12, 2017