The Centroid of a Triangle Divides Each Median in the Ratio 1:2
The Centroid of a Triangle Divides Each Median in the Ratio 1:2
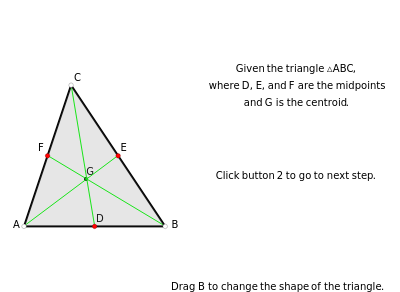
A median is the line from a midpoint of a side to the opposite vertex. The medians meet in the centroid, which is the center of mass of the triangle. A visual proof is given for the fact that the centroid of a triangle splits each of the medians in two segments, the one closer to the vertex being twice as long as the other one.
External Links
External Links
Permanent Citation
Permanent Citation
Tomas Garza
"The Centroid of a Triangle Divides Each Median in the Ratio 1:2"
http://demonstrations.wolfram.com/TheCentroidOfATriangleDividesEachMedianInTheRatio12/
Wolfram Demonstrations Project
Published: October 13, 2010